
[
на главную
]
Бустинг - композиции классификаторов
Е.С.Борисов
понедельник, 9 февраля 2015г.
1. Введение
При решении задачи классификации бывает, что ни один из применённых методов не даёт желаемого качества результата. Выходом из этого затруднения может быть построение композиции из этих методов, что бы они дополняли и исправляли ошибки друг-друга, например - простым голосованием. Важно что бы базовые классификаторы работали хоть немного лучше чем простое угадывание, т.е. количество правильных ответов должно быть больше количества ошибок.Рассмотрим учебный набор L=(X,Y) из множества точек (входов) X и множества ответов (выходов) Y .
Композицией t алгоритмов a i (x)=C(b i (x)) , i=1,...t называется суперпозиция алгоритмических операторов b i : X → R , корректирующей операции F : R t → R и решающего правила C : R → Y .
Пространство оценок R вводится для того, чтобы расширить множество допустимых корректирующих операций.
2. Алгоритм AdaBoost
В этом разделе мы поговорим о методе построения композиций, который получил название адаптивный бустинг или AdaBoost. Этот метод выполняет взвешенное голосование базовых алгоритмов, т.е. строит композицию следующего вида.
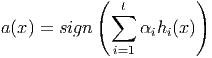
где α i - весовой коэффициент базового классификатора h i (x) .
Для построения композиции (обучения классификатора) каждой точке учебного множества ставится в соответствие вероятность ошибки P классификатора на данном примере. К композиции последовательно добавляются новые составляющие, на каждом шаге в зависимости от текущего значения ошибки обновляются вероятности P для точек учебного набора и вычисляется вес α для новой компоненты.
Алгоритм AdaBoost выглядит следующим образом.
-
инициализировать вероятности ошибок всех точек учебного набора
P i :=1/n где n - количество точек учебного набора, i=1,...n . - добавляем в композицию и обучаем новый базовый классификатор h(x) на учебном наборе L с учётом вероятностей ошибок P
-
вычисляем ошибку базового классификатора
h(x)
![e := ∑ P [h(x ) ⁄= y ]](/content/ml-adaboost.html/index3x.png)
-
если
e > 0.49
то ошибка превысила допустимый предел, переход на п. 10
иначе переход на следующий пункт -
если
e < e
min
то достигнут желаемый уровень качества, α:=1 , сохраняем h(x) , переход на п. 9
иначе переход на следующий пункт -
вычисляем вес для
h(x)
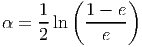
-
корректируем вероятности ошибок для точек учебного набора
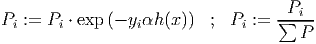
- сохраняем вес и параметры обученного базового классификатора h(x) , переход на п. 2
-
обучение завершено, нормируем веса
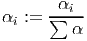
- конец работы
3. Реализация
В этом разделе описана реализация метода AdaBoost, в качестве базового классификатора h(x) используется пороговый классификатор (decision stump). Обучение h(x) сводится к простому перебору компонент учебного вектора и подбору для этих компонент значений порога дающих минимальную ошибку e на учебном наборе.Далее представлены результаты работы классификатора AdaBoost для 3 наборов данных. Каждый набор случайным образом разделяется на две равные части - учебную и тестовую.
Результаты для первого набора, общее количество точек - 200, на тесте ошибок нет.

|

|
| Рис.1: учебный набор | Рис.2: тестовый набор |

|

|
| Рис.3: результат работы | Рис.4: ошибки |
Результаты для второго набора, общее количество точек - 800, на тесте - 3 ошибки.

|
|
| Рис.5: учебный набор | Рис.6: тестовый набор |

|

|
| Рис.7: результат работы | Рис.8: ошибки |
Результаты для третьего набора, общее количество точек - 399, на тесте - 3 ошибки.

|

|
| Рис.9: учебный набор | Рис.10: тестовый набор |

|

|
| Рис.11: результат работы | Рис.12: ошибки |
Список литературы
-
Воронцов К.В. Композиции классификаторов
– http://shad.yandex.ru/lectures/machine_learning.xml - Yoav Freund, Robert E. Schapire. A decision-theoretic generalization of on-line learning and an application to boosting // Second European Conference on Computational Learning Theory. – 1995.
- Терехов С.А. Гениальные комитеты умных машин. IX Всероссийская научно-техническая конференция «Нейроинформатика–2007»: Лекции по нейроинформатике. часть 2. – М.: МИФИ, 2007. – 148 с.
