Байесовский классификатор

Евгений Борисов

вторник, 3 декабря 2013 г.

В этой статье мы рассмотрим математический метод, который называется байесовский классификатор.

1 Введение

Байесовский классификатор относится к методам машинного обучения ”с учителем”, но в отличии от перцептрона и других подобных моделей, он не требует длительной процедуры обучения. Можно сказать, что эта процедура в данном случае вырождена.

Классификатор содержит в себе учебную выборку для каждого класса и каждый вход последовательно сравнивается с этими наборами по определённому алгоритму, далее выбирается наиболее вероятный класс.

2 Принцип максимума апостериорной вероятности

Рассмотрим множество учебных примеров ( X,Y ) , здесь X ∋ x = ( ξ ₁ , … ,ξ _n ) – объекты, Y – классы. Классификатор должен отображать объекты в классы с минимальной вероятностью ошибки

a(x ) : X → Y

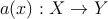
При этом предполагаем, что все признаки { ξ _i } объекта независимы друг от друга, из-за этого ограничения байесовский классификатор называют ”наивным”.

Байесовский классификатор основывается на принципе максимума апостериорной вероятности

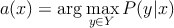
a(x) = arg mya∈xY P (y|x)

P ( y | x ) – вероятность события - x принадлежит классу y .

Согласно теореме об оптимальном байесовском классификаторе [ 1 ] , a ( x ) выглядит следующим образом

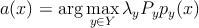
a (x ) = argmay∈xY λyPypy(x )

(1)

где λ _y – потеря при ошибочной классификации для класса y , будем считать, что в случае правильного ответа потерь нет, P ( y ) ≡ P _y – априорная вероятность класса y (определяется долей объектов x _y класса y в общем наборе X ), p _y ( x ) – плотность распределения x _y из класса y .

3 Восстановление плотности распределения

Для построения классификатора по ( 1 ) необходимо восстановить плотность распределения p _y по учебной выборке ( X,Y ) . Не будем здесь детально рассматривать методы восстановления плотностей и приведём сразу решение задачи, но прежде отметим важное обстоятельство. Поскольку мы приняли ограничение о независимости признаков ξ _i объектов x ∈ X то искомую n -мерную плотность можно рассматривать как произведение одномерных плотностей.

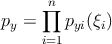
∏n py = pyi(ξi) i=1

Для восстановления плотности по выборке воспользуемся оценкой плотности Парзена-Розенблатта [ 1 ] .

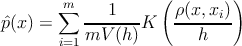
( ) m∑ ---1--- ρ-(x,-xi) ˆp(x) = mV (h)K h i=1

где m – количество элементов выборки X ∋ x _i , ρ – мера на X , h – окрестность x _i (”ширина окна”), K – функция ядра, V ( h ) – нормирующий множитель.

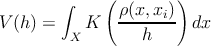
∫ ( ) V(h ) = K ρ(x,xi)- dx X h

В качестве функции ядра будем использовать ядро Епанечникова

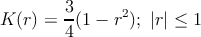
3 2 K (r) = 4-(1 − r); |r| ≤ 1

(2)

будем использовать Евклидову метрику

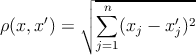
┌ ------------- ′ ││ ∑n ′ ρ(x,x ) = ∘ (xj − x j)2 j=1

(3)

Ещё необходимо выбрать ширину окна h . Этот параметр можно задавать разным способом. Здесь будем использовать метод скользящего контроля Leave One Out. Параметр h выбираем перебором, каждый раз проверяя суммарную ошибку на учебном множестве, при этом из учебного набора удаляется текущий (проверяемый) пример.

∑l LOO (h,X ) = [a(xi;{X ∕xi},h) ⁄= yi] → min i=1 h

4 Байесовский классификатор

В конечном итоге классификатор описывается следующим соотношением.

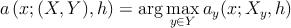
a(x;(X, Y ),h) = argmayx∈Y ay(x;Xy, h)

где ( X,Y ) - учебная выборка, λ _y - коэффициент потерь на классе y , P _y - априорная вероятность y , l _y - количество объектов x в классе y , ρ – мера ( 3 ) на X , K – функция ядра ( 2 ).


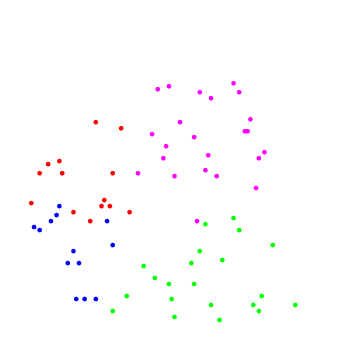
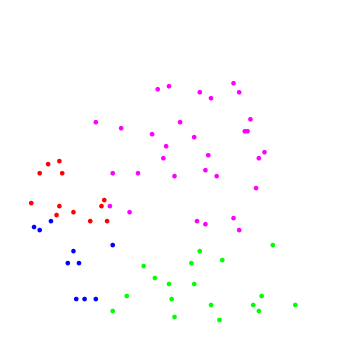
Рис.1: учебный набор	Рис.2: результат работы

Реализация в системе Octave [ здесь ].

Список литературы

[1] Воронцов К.В. Статистические методы классификации – http://shad.yandex.ru/lectures/machine_learning.xml

[2] GNU Octave – http://www.gnu.org/software/octave/

При использовании материалов этого сайта, пожалуйста вставляйте в свой текст ссылку на мою статью.