
Классификатор изображений на основе свёрточной сети.
Е.С.Борисов
понедельник, 9 мая 2016 г.
В этой статье мы поговорим методе классификации, который носит название свёрточная нейронная сеть. Этот метод ориентирован на работу с изображениями, но может использоваться для распознавания звуковых образов и не только.
1 Введение
Свёрточная нейронная сеть (convolutional neural network, CNN, LeNet) была представлена в 1998 году французским исследователем Яном Лекуном (Yann LeCun) [ 1 ] , как развитие модели неокогнитрон (neocognitron) [ 2 ] .
Модель свёрточной сети, которую мы рассмотрим в этой статье, состоит из трёх типов слоёв: свёрточные (convolutional) слои, субдискретизирующие (subsampling,подвыборка) слои и слои "обычной"нейронной сети – перцептрона [ 3 ] .
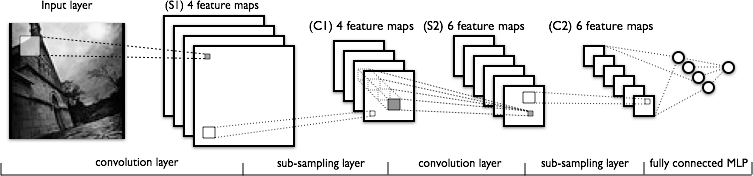
Рис.1: схема свёрточной сети (с сайта http://deeplearning.net)
Первые два типа слоёв (convolutional,subsampling), чередуясь между собой, формируют входной вектор признаков для многослойного перцептрона. Сеть можно обучать с помощью градиентных методов [ 4 ] .
Своё название свёрточная сеть получила по названию операции – свёртка [ 5 ] , она часто используется для обработки изображений и может быть описана следующей формулой.
![∑ (f ∗ g)[m, n ] = f [m − k,n − l] ⋅ g [k,l] k,l](/content/ml-lenet.html/index0x.png)
Здесь f - исходная матрица изображения, g - ядро (матрица) свёртки.
Неформально эту операцию можно описать следующим образом - окном размера ядра g проходим с заданным шагом (обычно 1) всё изображение f , на каждом шаге поэлементно умножаем содержимое окна на ядро g , результат суммируется и записывается в матрицу результата.
При этом в зависимости от метода обработки краёв исходной матрицы результат может быть меньше исходного изображения (valid), такого же размера (same) или большего размера (full).
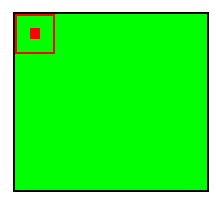
Рис.2: обработка краёв valid |
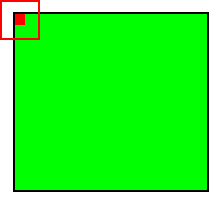
Рис.3: обработка краёв same |
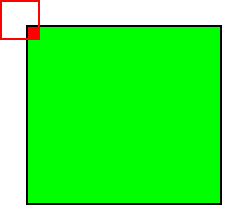
Рис.4: обработка краёв full |
2 Свёрточный слой
В этом разделе мы рассмотрим устройство свёрточного слоя.
Свёрточный слой реализует идею т.н. локальных рецептивных полей, т.е. каждый выходной нейрон соединен только с определённой (небольшой) областью входной матрицы и таким образом моделирует некоторые особенности человеческого зрения.
В упрощённом виде этот слой можно описать следующей формулой.
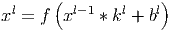
Здесь x l - выход слоя l , f () - функция активации, b - коэффициент сдвига, символом ∗ обозначена операция свёртки входа x с ядром k .
При этом за счёт краевых эффектов размер исходных матриц уменьшается.
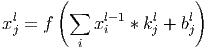
Здесь x j l - карта признаков j (выход слоя l ), f () - функция активации, b j - коэффициент сдвига для карты признаков j , k j - ядро свёртки номер j , x i l − 1 - карты признаков предыдущего слоя.
3 Субдискретизирующий слой
В этом разделе мы поговорим про субдискретизирующий (subsampling) слой. Слои этого типа выполняют уменьшение размера входной карты признаков (обычно в 2 раза). Это можно делать разными способами, в данном случае мы рассмотрим метод выбора максимального элемента (max-pooling) - вся карта признаков разделяется на ячейки 2х2 элемента, из которых выбираются максимальные по значению. Формально слой может быть описан следующим образом.
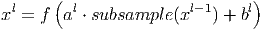
Здесь x l - выход слоя l , f () - функция активации, a,b - коэффициенты, subsample () - операция выборки локальных максимальных значений.
Использование этого слоя позволяет улучшить распознавание образцов с изменённым масштабом (уменьшенных или увеличенных).
4 Слой MLP
Последний из типов слоёв это слой ”обычного” многослойного перцептрона (MLP), его можно описать следующим соотношением.
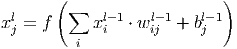
Здесь x l - выход слоя l , f () - функция активации, b - коэффициент сдвига, w - матрица весовых коэффициентов.
5 О топологии сети
В этом разделе мы поговорим о схеме соединения слоёв между собой.
Рассмотрим свёрточную сеть из 7 слоёв, порядок их следования описан ниже.
- входной слой - матрица картинки
- свёрточный слой - набор однотипных матриц (карт признаков)
- субдискретизирующий слой - уменьшенный в 2 раза предыдущий набор матриц
- свёрточный слой - предыдущий набор матриц объединяется в одну, в соответствии со схемой соединения слоёв, и генерируется новый набор
- субдискретизирующий слой - уменьшенный в 2 раза предыдущий набор матриц
- слой MLP - предыдущий набор матриц разворачивается в вектор и обрабатывается как MLP
- слой MLP (выходной)
При этом, нейроны (карты признаков) второго субдискретизирующего слоя и третьего свёрточного слоя соединяются выборочно т.е. в соответствии с матрицей смежности, которая задаётся как параметр сети. Для сети с количеством карт признаков во втором слое 7 и 9 в третьем слое, она может выглядеть следующим образом.

Таблица 1: пример матрицы смежности связей свёрточных слоёв
Таким образом, каждая выходная карта формируеться частичной суммой результатов свёрток входных карт, для каждой такой частичной суммы свой набор ядер свёртки.
6 Метод обучения сети
Для обучения свёрточной сети применяются градиентные методы [ 4 , 6 ] .
6.1 Вычисление ошибки
Для выходного (MLP) слоя ошибка рассчитывается следующим образом.
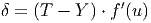
Здесь T - ожидаемый (учебный) выход , Y - реальный выход, f ′ ( u ) - производная функции активации по её аргументу
Для скрытых слоёв MLP ошибка имеет следующий вид.
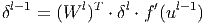
Здесь δ l - ошибка слоя l , f ′ ( u l ) - производная функции активации, u l - состояние (не активированное) нейронов слоя l , W l - матрица весовых коэффициентов слоя l .
Ошибка на выходе свёрточного слоя формируется путём простого увеличения размера матриц ошибки следующего за ним субдискретизирующего слоя.
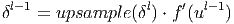
Здесь δ l - ошибка слоя l , f ′ ( u l ) - производная функции активации, u l - состояние (не активированное) нейронов слоя l , upsample () - операция увеличения размера матриц.
Ошибка на выходе субдискретизирующего слоя рассчитывается путём выполнения ”обратной свёртки” карт признаков следующего за ним свёрточного слоя, т.е. над каждой картой признаков выполняется свёртка с соответствующим ”перевернутым” ядром, при этом за счёт краевых эффектов размер исходных матриц увеличивается. Далее над получившимися картами вычисляются несколько частичных сумм по числу ядер свертки, в соответствии с матрицей смежности субдискретизирующего и свёрточного слоёв.
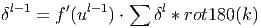
Здесь δ l - ошибка слоя l , f ′ ( u l ) - производная функции активации, u l - состояние (не активированное) нейронов слоя l , k - ядра свёртки.
6.2 Вычисление градиента
В этом разделе описана процедура вычисления градиента функции потери сети, т.е. направления максимального роста функции потери. Обучение сводиться к её минимизации в пространстве параметров (весов) сети.
-
Градиент для ядра свёртки можно посчитать как свёртку
матрицы входа свёрточного слоя с "перевёрнутой" матрицей
ошибки для выбранного ядра.
Здесь δ l - ошибка слоя l , x l - вход слоя l , k - ядра свёртки.
Градиент для сдвига для свёрточного слоя вычисляется как сумма значений соответствующей матрицы ошибки.
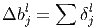
Здесь δ l - ошибка слоя l
-
Градиент для коэффициентов субдискретизирующего слоя
вычисляется следующим образом.
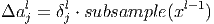
Здесь x l - выход слоя l , δ l - ошибка слоя l , subsample () - операция выборки локальных максимальных значений.
Градиент для коэффициента сдвига для субдискретизирующего слоя вычисляется как сумма значений соответствующей матрицы ошибки.
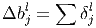
Здесь δ l - ошибка слоя l
-
Градиент для весов MLP выглядит следующим образом.
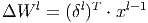
Здесь δ l - ошибка слоя l , x l - вход слоя l , W l - матрица весовых коэффициентов слоя l .
7 Реализация
В этом разделе описана реализация классификатора рукописных символов на основе свёрточной сети. В качестве учебного набора была использована база MNIST [ 7 ] , которая содержит 60 тысяч учебных образов с цифрами от 0 до 9 разного начертания.
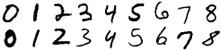
Рис.5: образцы из базы MNIST
Обучение заняло несколько часов. Конечная средня квадратическая ошибка (MSQE) обучения 0.076052.
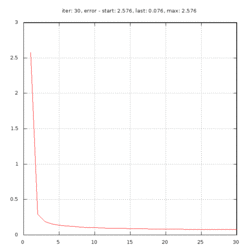
Рис.6: график изменения ошибки обучения
Проверка итогового качества обучения проводилась на наборе из 10 тысяч образов. Средня квадратическая ошибка на тестах 0.072857 или 344 ошибок и отказов на 10000.


Рис.8: примеры тестов, давших ошибочный результат
Результат можно улучшить подобрав оптимальные параметры сети.
Она состоит из трёх частей.
- конвертер БД MNIST в формат системы,
- программа обучения сети, генерирующая рабочие веса классификатора,
- и программа-тест, которая тестирует обученную сеть на конвертированных примерах из БД MNIST.
Сам набор данных MNIST можно скачать на сайте [ 7 ] .
7.1 Реализация для Caffe
В этом разделе представлена реализация свёрточной сети в системе Caffe [ 8 ] .Caffe является системой моделирования свёрточных сетей, она может использовать для вычислений GPU [ 9 ] и работает гораздо быстрее чем представленная выше реализация свёрточной сети на octave, обучение с использованием GPU занимает меньше минуты.
Caffe имеет привязки для нескольких популярных языков программирования, мы будем использовать python. Для того чтобы построить и обучить сеть с помощью Caffe вообще не обязательно писать программный код, достаточно описать модель в спецификации.
Для спецификаций используется язык protobuf [ 10 ] . Спецификация состоит из трех следующих файлов, которые можно найти в пакете caffe в каталоге примеров.
-
train_test.prototxt
- описание сети и данных для обучения, ниже представлена схема сети (кликабельно)
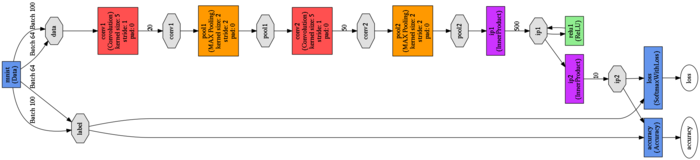
-
solver.prototxt
- параметры метода обучения
-
deploy.prototxt
- описание уже обученной сети для использования в классификаторе,
ниже представлена схема сети (кликабельно)

- входной слой
- свёрточный слой
- слой выборки (max-pooling)
- свёрточный слой
- слой выборки (max-pooling)
- слой MLP с активацией ReLu
- слой MLP с активацией SoftMax
Реализация для Caffe [ здесь ].
Список литературы
[1] LeCun, Yann. "LeNet-5, convolutional neural networks". – http://yann.lecun.com/exdb/lenet/
[2] Fukushima Kunihiko Neocognitron: A Self-organizing Neural Network Model for a Mechanism of Pattern Recognition Unaffected by Shift in Position. // Biological Cybernetics 1980 36 (4)
[3]
Борисов Е. Классификатор на основе многослойной нейронной
сети.
– http://www.mechanoid.kiev.ua/neural-net-perceptron-multi-layer-classifier.html
[4]
Борисов Е. О методах обучения многослойных нейронных сетей прямого распространения.
– http://www.mechanoid.kiev.ua/neural-net-backprop.html
[5]
Борисов Е. Базовые методы обработки изображений.
– http://www.mechanoid.kiev.ua/cv-base.html
[6]
Jake Bouvrie Notes on Convolutional Neural Networks
– http://cogprints.org/5869/1/cnn_tutorial.pdf
[7]
The MNIST database of handwritten digits
– http://yann.lecun.com/exdb/mnist/
[8]
Caffe - deep learning framework
– http://caffe.berkeleyvision.org
[9]
Борисов Е. Технология параллельного программирования CUDA
– http://mechanoid.home.lan/parallel-cuda.html
[10]
Google Protocol Buffers
– http://developers.google.com/protocol-buffers/