1 Введение

В этой статье мы поговорим о методах математической регрессии. Регрессия это восстановление зависимости между переменными по набору данных или условное математическое ожидание при заданном параметре[1,2].

Методы регрессии можно использовать для предсказания значения переменной. Например, пусть у нас есть простая статистика продаж домов из двух параметров – площадь и цена. На основании этих данных необходимо оценить дом с известной площадью. Эту задачу можно решить построив регрессию на данном наборе данных [3]. Не формально говоря, нам надо нарисовать линию (определить функцию), проходящую через облако точек. После этого вычислить значение этой функции в искомой точке.

2 Линейная регрессия

Первый метод, который мы рассмотрим, это линейная регрессия. Линейная потому, что искомая функция в данном случае линейна.

Рассмотрим набор данных из m элементов размера n + 1

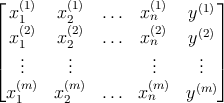
Наша функция (или гипотеза) задаётся следующим образом

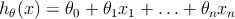
где 𝜃 ₀ ,𝜃 ₁ , … ,𝜃 _n – параметры

или в векторном виде

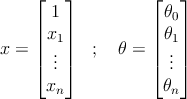
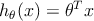
Задача построения регрессии сводиться к определению коэффициентов 𝜃 . Неформально, нам необходимо нарисовать линию проходящую через центр облака точек, и по возможности минимально удалённую от каждой из этих точек.

2.1 Аналитический метод

Для некоторых наборов данных эти коэффициенты можно вычислить аналитически следующим образом.

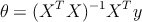
где

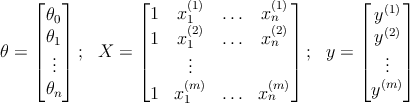
Этот метод можно применять для относительно небольших наборов данных. Возможны варианты когда X ^T X необратимая (вырожденная) матрица, это может получиться если свойства x _j ^{( i )} линейно зависимы или/и мало данных и много свойств x _j ^{( i )} , т.е. n > m .

Реализация в системе Octave [ здесь ].

2.2 Метод градиентного спуска

Для наборов данных, на которых по какой-то причине не работает аналитический метод, для построения линейной регрессии можно применить метод итеративный. Для этого нам нужно определить функцию стоимости (оценки, cost function), в качестве неё будем использовать квадратичную ошибку (squared error):

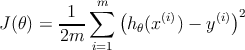
Нам необходимо подобрать набор коэффициентов 𝜃 , который бы минимизировал функцию стоимости

Для решения этой задачи можно использовать метод градиентного спуска (gradient descent). Алгоритм выглядит следующим образом.

1. инициализировать 𝜃 = (0 , 1 , … 1)
2. вычислить значение h _𝜃 ( x ) для всех входов
3. вычислить значение функции стоимости J ( 𝜃 )
4. если значение функции стоимости J ( 𝜃 ) меньше порога
   то обучение завершено, перейти на п. 7
   иначе перейти на следующий пункт
5. изменить значения 𝜃
   где 0 < α < 1 – параметр (скорость обучения)

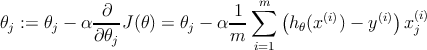
6. перейти на п. 2
7. конец работы

Рис. 1: линейная регрессия: аналитический метод

Рис. 2: линейная регрессия: градиентный спуск

2.3 Нелинейная регрессия

Для улучшения результата, в качестве гипотезы h _𝜃 ( x ) можно использовать нелинейные функции. Например кубический полином:

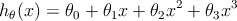
Алгоритм обучения здесь почти такой же как и для линейной регрессии только изменение коэффициентов 𝜃 для процедуры градиентного спуска будет выглядеть следующим образом.

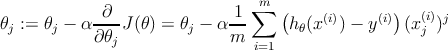
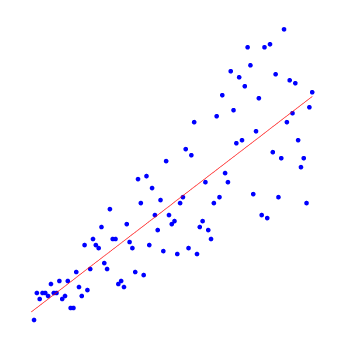
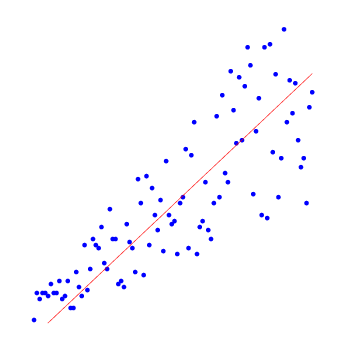
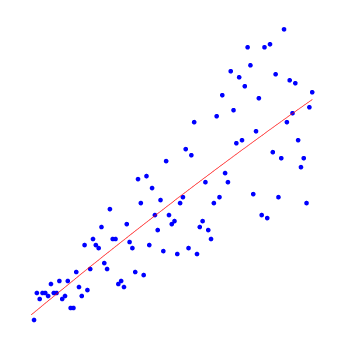
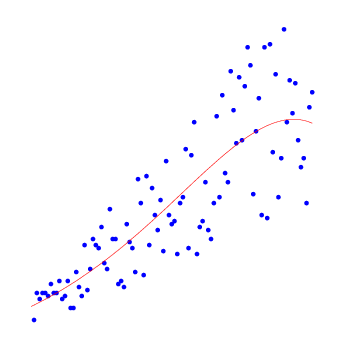
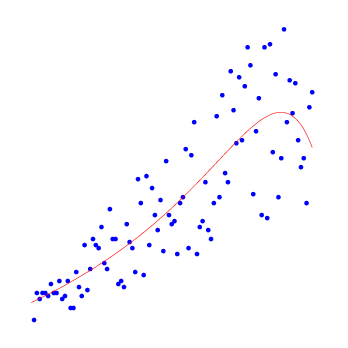
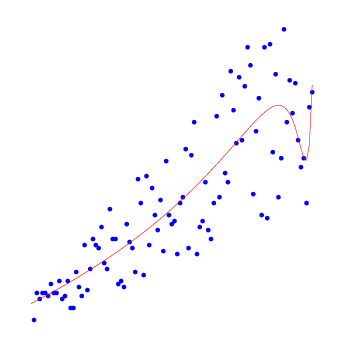
Приведём примеры результатов работы алгоритма нелинейной регрессии для полиномов разных степеней.

Рис. 3: нелинейная регрессия: полином 2 степени	Рис. 4: нелинейная регрессия: полином 5 степени
Рис. 5: нелинейная регрессия: полином 12 степени	Рис. 6: нелинейная регрессия: полином 72 степени

Реализация в системе Octave [ здесь ].

Список литературы

При использовании материалов этого сайта, пожалуйста вставляйте в свой текст ссылку на мою статью.