О методах обучения
многослойных нейронных сетей
прямого распространения.

Часть 1: Общие положения.

Е.С.Борисов

пятница, 12 февраля 2016 г.

В этой статье мы поговорим о методах обучения классификатора на основе искусственных нейронных сетей прямого распространения, т.е. сетей не имеющих обратных связей.

1. Введение.

Многие практические задачи сводятся к выбору объектов из их множества. Например технический контроль различных устройств - выявление брака и диагностика неисправностей. Этот выбор можно делать случайным образом, а можно сформулировать некоторые критерии (признаки) и правила отбора на основе этих признаков. В качестве признаков могут выступать самые разные свойства рассматриваемой предметной области: содержание кислорода, цвет поверхности, длинна стебля, частота повторения слова в тексте. Таким образом, каждому объекту в рамках задачи ставится в соответствие упорядоченный набор определённых величин или вектор-признак.

Построив формальное пространство признаков мы можем применить математические методы классификации для разделения множества объектов на части или классы.

Формально это можно записать следующим образом. $$ f : O \rightarrow X $$ $$ h : X \rightarrow C $$ где
$O$ - множество объектов задачи,
$f$ - функция отбора признаков (feature extractor),
$X\ni(x_1\ldots,x_n)$ - пространство признаков размерности $n$,
$C$ - множество классов,
$h$ - функция выбора (классификатор).

Далее мы рассмотрим задачу обучения классификатора.

2. Стратегии обучения классификатора.

Классификатор $h$ можно строить разными способами, например его параметры можно попробовать подобрать вручную в виде пороговых правил типа $(x_1 \gt 0) \land (x_2 \lt 4) \lor (x_3 \neq 0.5) $, однако при большом количестве объектов и их признаков такое решение трудно реализовать. Поэтому для конструирования классификаторов обычно применяют более сложные методы.

Настройка определённым способом параметров классификатора на основе набора данных называют обучением классификатора .

Для обучения классификатора нам понадобится размеченный (учебный) набор данных, т.е. множество пар $(X,C)_L$. Классификатору предъявляются по очереди учебные примеры из $X$, ответ классификатора $Y$ сравнивается с правильным ответом $C$ и по результатам сравнения корректируются параметры классификатора. Такая схема настройки классификатора называется "обучение с учителем" , более строго это выглядит так.

1. обрабатываем учебный набор
2. определяем ошибки
3. если результат удовлетворительный то конец работы
4. корректируем параметры
5. переход на п.1

При таком подходе может проявится эффект переобучения (overfitting), когда классификатор хорошо обрабатывает только учебное множество, но на остальных объектах результаты значительно хуже (плохое обобщение).

Для борьбы с переобучением набор для тренировки классификатора разделяют на три части: учебный, контрольный, тестовый.

• Учебный набор применяют для корректировки параметров,
• контрольный - для текущей оценки состояния,
• тестовый - для оценки итогового результата обучения.

Для улучшения результатов можно применять различные стратегии коррекции параметров: полную, частичную или стохастическую, т.е. на каждом цикле обучения (эпохе) можно обрабатывать не все примеры а только их часть. Эти стратегии можно описать следующим образом:

• Полная (full batch) - на каждом цикле прогоняется всё учебное множество.
  1. обрабатываем учебный набор
  2. определяем ошибки
  3. корректируем параметры
  4. проверка на контрольном множестве
  5. если результат удовлетворительный то выполняем итоговый тест и конец работы
  6. переход на п.1
• Частичная (mini batch) - на каждом цикле используется случайно выбранное подмножество учебного набора
  1. случайным образом выбрать подмножество учебного набора
  2. обрабатываем эту часть учебного набора
  3. определяем ошибки
  4. корректируем параметры
  5. проверка на контрольном множестве
  6. если результат удовлетворительный то выполняем итоговый тест и конец работы
  7. переход на п.1
• Стохастическая (stochastic) - на каждом цикле случайно выбирается один пример,
  1. случайным образом выбрать пример из учебного набора
  2. обработать этот пример
  3. определяем ошибку
  4. сохраняем текущее состояние параметров
  5. определяем новые параметры
  6. проверка на контрольном множестве
  7. если результат удовлетворительный то выполняем итоговый тест и конец работы
  8. если ошибка выросла
     то с вероятностью пропорциональной величине прироста ошибки
     выполняется откат к предыдущему состоянию параметров
  9. переход на п.1

Далее мы рассмотрим модель классификатора, который называется многослойная нейронная сеть. Эта модель представляет собой многомерную функцию. $$ (y_1\ldots,y_m)=h(x_1\ldots,x_n) $$ С её помощью можно апроксимировать (повторить с некоторой точностью) функцию заданную точками учебного множества (задачи прогнозирования), а так же строить разделяющие поверхности в пространстве признаков, отделяя объекты одного класса от объектов других классов (задачи классификации).

В следующем разделе мы разберём её подробней.

3. Многослойная нейронная сеть прямого распространения.

Искусственная нейронная сеть (рис.1) состоит из элементов называемых математическими нейронами . Математический нейрон (рис.2) имеет несколько входов и один выход, формально это можно описать следующим образом (\ref{eq:neuron}).
\begin{equation} y=f(s)\ ;\ s=\sum_i w_i x_i + w_0 \label{eq:neuron} \end{equation}

На вход нейрона поступают сигналы $x_1,\ldots x_n$, каждый вход имеет вес $w_i$, при этом $x_0\equiv 1$ и $w_0$ называют сдвигом . Линейная комбинация входов $s$ называется состоянием нейрона .

Рис.1: схема многослойной нейронной сети прямого распространения.	Рис.2: схема искусственного нейрона.

Функция $f$ называется функцией активации нейрона. Она может иметь разный вид, приведём примеры.

Рис.: гиперболический тангенс (сигмоид) $\ y=\tanh(s)=\frac{\exp(s) - \exp(-s)}{\exp(s)+\exp(-s)}$

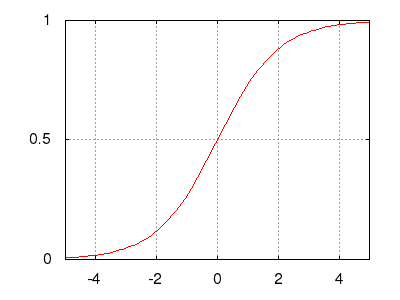
Рис.: экспоненциальный сигмоид $\ y=\frac{1}{1+\exp(-s)}=\frac{\exp(0)}{\exp(0)+\exp(-s)}$

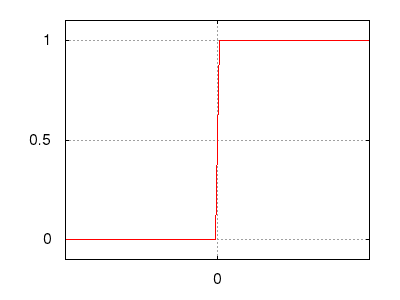
Рис.: пороговая функция $\ y=[ s\gt0 ]$	Рис.: rectified linear unit (ReLU) $\ y=max(0,s)$

Нейроны, составляющие сеть, разбиты на группы называемые слоями . В сетях прямого распространения сигнал проходит послойно в одном направлении - от входа к выходу. Нейроны одного слоя активируются одновременно, каждый нейрон может иметь связи с нейронами следующего слоя, связь нейрона на самого себя (петли) и/или связи с предыдущими слоями (обратные связи) в этой схеме отсутствуют.

Первый слой называется входным или распределительным , нейроны этого слоя не изменяют сигнал и просто распределяют его нейронам второго слоя. Второй и следующие за ним слои называются обрабатывающими и выполняют работу по преобразованию входного сигнала.

Кроме функций активации нейронов, описанных выше, можно использовать совместную активацию нейронов слоя, например функция активации softmax (экспоненциальная нормализация), её обычно используют для выходного слоя. $$ (y_1,\ldots,y_m) = softmax(s_1,\ldots,s_m) = \frac{\exp(s)}{\sum\limits_j \exp(s_j)} $$

Также стоит упомянуть стохастическую модель, здесь функция активации $f(s)$ принимает значение $1$ с вероятностью $p=1/(1+\exp(-s))$ или соответственно значение $0$ с вероятностью $1-p$.

Далее мы рассмотрим методы обучения многослойной нейронной сети.

4. Функция потери и настройка весов нейронной сети.

Обучение нейронной сети, описанной выше, это настройка весов $W$ в соответствии с учебным множеством $(X,C)$ и важным элементом этой процедуры является способ оценки работы сети или функция потери (loss function) $E$. $$ h : X\times W \rightarrow Y $$ $$ E : Y\times C \rightarrow \mathbb{R} $$ где
$h$ - классификатор,
$W$ - веса сети,
$X\ni(x_1\ldots,x_n)$ - пространство признаков размерности $n$,
$E$ - функция потери,
$Y$ - выход классификатора,
$C$ - множество правильных ответов (номеров классов).

В качестве функции потери для нейронных сетей обычно используется среднеквадратичная ошибка (MSQE) $$ E=\frac{1}{2}\sum\limits_j (y_j-c_j)^2 $$ где $y_j$ - выход сети номер $j$, $c_j$ - правильный ответ для выхода $j$

Но MSQE это не единственный вариант, для сетей с выходным слоем softmax обычно используют среднюю кросс-энтропию по всем учебным примерам. $$ E= \frac{1}{k}\sum\limits_{i=1}^k\left(-log(p_i)\right); $$ где $k$ - количество примеров, $p_i$ - выданная классификатором вероятность принадлежности примера $X_i$ к своему классу $C_i$.

Введя функцию потери $E$, мы теперь можем формально поставить задачу обучения классификатора $h$ следующим образом - процедура обучения нейронной сети это минимизация функции потери в пространстве весов. \begin{equation} \min_W E(h(X,W),C) \label{eq:ermin} \end{equation}

Во второй части этой статьи мы займёмся решением этой задачи.

Список литературы

1. Е.С.Борисов Основные модели и методы теории искусственных нейронных сетей. - http://www.mechanoid.kiev.ua
2. Осовский С. Нейронные сети для обработки информации. — М.: Финансы и статистика, 2002.

При использовании материалов этого сайта, пожалуйста вставляйте в свой текст ссылку на мою статью.