
[
на главную
]
О методах обучения
многослойных нейронных сетей
прямого распространения.
Часть 2: Градиентные методы первого порядка.
Е.С.Борисовчетверг, 21 апреля 2016 г.
Этот текст является прололжением статьи о методах обучения многослойных нейронных сетей прямого распространения. Здесь мы поговорим о градиентных методах первого порядка обучения классификатора.
1. Введение.
В предыдущей статьи мы формально поставили задачу обучения классификатора $h$ как минимизацию функции потери в пространстве весов. \begin{equation} \min_W E(h(X,W),C) \label{eq:ermin} \end{equation}Далее мы займёмся решением этой задачи.
2. Градиентные методы обучения первого порядка
Для решения задачи (\ref{eq:ermin}), мы будем использовать градиентные методы оптимизации (первого порядка). Градиент функции $\nabla E(W)$ в точке $W$ это направление наискорейшего её возрастания, соответственно для минимизации функции необходимо изменять параметры в сторону противоположную градиенту. Этот подход называется методом градиентного спуска . Общая схема такого обучения выглядит следующим образом.
- инициализировать веса $W$ (случайными малыми значениями)
- вычисляем ошибку $E(h(X,W),C)$
- если результат удовлетворительный то конец работы
- вычисляем значение градиента ф-ции потери: $\nabla E(h(X,W),C)$
- вычисляем изменение параметров: $\Delta W = \eta\cdot \nabla E$
- корректируем параметры: $W:=W-\Delta W$
- переход на п.2
Таким образом, следующая задача, которую необходимо решить для реализации обучения нейронной сети, это найти способ вычисления градиента функции потери $\nabla E(h(X,W),C)$.
3. Метод обратного распространения ошибки.
Для решения задачи оптимизации (\ref{eq:ermin}) методом градиентного спуска, описанном в предыдущем разделе, нам необходимо найти способ вычисления градиента функции потери $\nabla E$, который представляет собой вектор частных производных. $$\nabla E(W) = \left[ \frac{\partial E}{\partial w_1}\ldots, \frac{\partial E}{\partial w_k} \right]$$ где $k$ - общее количество весов сети.Для случая нейронной сети градиент можно записать следующим образом. \begin{equation} \frac{\partial E}{\partial w_{ij}} = \frac{\partial E}{\partial y_j} \frac{\partial y_j}{\partial s_j} \frac{\partial s_j}{\partial w_{ij}} \label{eq:grad} \end{equation}
где $E$ - функция потери, $w_{ij}$ - вес связи нейронов $i$ и $j$, $y_j$ - выход нейрона номер $j$, $s_j$ - состояние нейрона $j$.
Рассмотрим части соотношения ($\ref{eq:grad}$) отдельно :
$\partial s_j/\partial w_{ij}$ - выход $i$-того нейрона предыдущего (по отношению к нейрону $j$) слоя, эта часть определена в явном виде,
$\partial y_j/\partial s_j$ - значение производной активационной функции по ее аргументу для нейрона $j$, эту часть достаточно просто можно вычислить,
$\partial E/\partial y_j$ - ошибка нейрона номер $j$, здесь возникают некоторые затруднения. Значения ошибки определены явно только для нейронов выходного слоя, как быть со скрытыми слоями? Здесь нам поможет способ, который носит название - метод обратного распространения ошибки .
Суть его заключается в последовательном вычислении ошибок скрытых слоёв с помощью значений ошибки выходного слоя, т.е. значения ошибки распространяются по сети в обратном направлении от выхода к входу.
Здесь мы не будем приводить вывод формул, сразу приведём результат - рекурсивную формулу для расчетов величины $\partial E/\partial y$ :
для выходного слоя $$ \delta_i := \frac{\partial E}{\partial y_i} $$ для скрытого слоя \begin{equation} \delta_i := \frac{\partial y_i}{\partial s_i}\cdot \sum\limits_j \delta_j w_{ij} \label{eq:bper} \end{equation} где $\partial y/\partial s$ - значения производной активационной функции по ее аргументу.
Сам алгоритм расчёта градиента функции потери методом обратного распространения ошибки выглядит следующим образом.
- прямой проход: вычислить состояния нейронов $s$ всех слоёв и выход сети
- вычисляем значения $\delta := \partial E/\partial y$ для выходного слоя
- обратный проход: последовательно от конца к началу для всех скрытых слоёв вычисляем $\delta$ по формуле ($\ref{eq:bper}$)
-
для каждого слоя вычисляем значение градиента $\nabla E = \partial E/ \partial W = y \cdot \delta^T$,
где $y$ - вектор-вход слоя, $\delta$ - вектор ошибки на выходе слоя.
4. Метод градиентного спуска
Выше мы уже приводили схему метода градиентного спуска, здесь будет представлена его немного усложнённая версия, этот алгоритм является базовым для алгоритмов описанных в следующих разделах.Метод градиентного спуска в "чистом" виде может "застревать" в локальных минимумах функции потери $E$, для борьбы с этим мы будем использовать несколько дополнений для этого метода. Первое дополнение это применение уже описанной выше стратегии mini-batch, а второе это так называемые "моменты".
Метод моментов можно сравнить с поведением тяжёлого шарика, который скатываясь по склону в ближайшую низину некоторое расстояние способен двигаться вверх по инерции, выбираясь таким образом из локальных минимумов. Формально это выглядит как добавка для изменения весов сети. $$ \Delta W_t := \eta\cdot \nabla E + \mu \cdot \Delta W_{t-1} $$ где $\eta$ - коэффициент скорости обучения,
$\nabla E$ - градиент функции потери,
$\mu$ - коэффициент момента,
$\Delta W_{t-1}$ - изменение весов на предыдущей итерации.
Ещё одним усовершенствованием метода оптимизации будет применение регуляризации. Регуляризация "накладывает штраф" на чрезмерный рост значений весов это помогает бороться с переобучением . Формально это выглядит ещё одна добавка для изменения весов сети. $$ \Delta W_t := \eta\cdot \left( \nabla E + \rho \cdot W_{t-1} \right) + \mu \cdot \Delta W_{t-1} $$ где $\eta$ - коэффициент скорости обучения,
$\nabla E$ - градиент функции потери,
$\mu$ - коэффициент момента,
$\Delta W_{t-1}$ - изменение весов на предыдущей итерации,
$\rho$ - коэффициент регуляризации,
$W_{t-1}$ - значения весов на предыдущей итерации.
Так же мы будем изменять коэффициент скорости обучения $\eta$ на каждой итерации $t$ в зависимости от изменения ошибки $E$ следующим образом.
$$ \eta_t = \left\{\begin{array}{ l c c } \alpha\cdot \eta_{t-1} & : & \Delta E \gt 0 \\ \beta\cdot \eta_{t-1} & : & - \end{array} \right. $$ где $\eta_0 = 0.01$ - начальное значение скорости обучения,
$ \Delta E = E_t - \gamma \cdot E_{t-1} $ - изменение ошибки,
$\alpha=0.99,\ \beta=1.01,\ \gamma=1.01$ - константы
Таким образом, при существенном росте ошибки $E$ шаг изменения параметров $\eta$, уменьшается, в противном случае - шаг $\eta$ увеличивается. Это дополнение может увеличить скорость сходимости алгоритма.
Соберём всё вместе, наш алгоритм приобретает следующий вид.
- инициализировать веса $W$ (случайными малыми значениями)
- инициализировать нулями начальные значение изменения весов $\Delta W$
- вычисляем ошибку $E(h(X,W),C,W)$ и её изменение $\Delta E$ на контрольном наборе
- если результат удовлетворительный то то выполняем итоговый тест и конец работы
- случайным образом выбрать подмножество $(X,C)_L$ из учебного набора
- вычисляем значение градиента функции потери $\nabla E$ на выбранном подмножестве
- вычисляем изменение параметров: $\Delta W := \eta\cdot ( \nabla E + \rho \cdot W )+ \mu \cdot \Delta W $
- корректируем параметры: $W:=W-\Delta W$
- корректируем скорость обучения $\eta$
- переход на п.3
5. Метод quickProp
В этом разделе мы рассмотрим модификацию описанного в предыдущем разделе метода градиентного спуска, которая называется quickProp . От базового метода он отличается тем, что параметр момента $\mu$ и коэффициент скорости обучения $\eta$ задаются индивидуально для каждого параметра. Изменение параметров описывается следующим соотношением. $$ \Delta W := \eta\cdot ( \nabla E + \rho \cdot W ) + \mu \cdot \Delta W $$ где $\rho$ - коэффициент регуляризации.Параметр скорости обучения вычисляется следующим образом. $$ \eta = \left\{\begin{array}{ l c c } \eta_0 & : & (\Delta W = 0) \lor ( -\Delta W \cdot S \gt 0) \\ 0 & : & - \end{array} \right. $$ где $\eta_0 \in (0.01 , 0.6) $ - константа, $S = \nabla E + \rho W$
Параметр момента выглядит следующим образом. $$ \mu = \left\{\begin{array}{ l c c } \mu_{max} & : & (\beta \gt \mu_{max}) \lor (\gamma \lt 0) \\ \beta & : & - \end{array} \right. $$ где $\mu_{max}=1.75$ - константа,
$S = \nabla E + \rho W$,
$\beta = S(t) / ( S(t-1) - S(t) ) $
$ \gamma = S \cdot (-\Delta W) \cdot \beta $
Далее построим реализацию и посмотрим как это работает.
6. Метод rProp
В этом разделе мы рассмотрим модификацию описанного в предыдущем разделе метода градиентного спуска, которая называется rProp (resilient back propagation). В случае rProp моменты и регуляризация не используются, применяется простая стратегия full-batch . Ключевую роль играет параметр скорости обучения $\eta$, он рассчитывается для каждого веса индивидуально. $$ \eta(t) = \left\{\begin{array}{ l c c } min( \eta_{max}, a\cdot \eta(t-1) ) & : & S \gt 0 \\ max( \eta_{min}, b\cdot \eta(t-1) ) & : & S \lt 0 \\ \eta(t-1) & : & S = 0 \end{array} \right. $$ где $S=\nabla E(t-1)\cdot \nabla E(t)$ - произведения значений градиента на этом и предыдущем шаге,$ \eta_{max}=50\ ,\ \eta_{min}=10^{-6}\ ,\ a=1.2\ ,\ b=0.5 $ - константы
Изменение параметров выглядит следующим образом.
$$ \Delta W_t := \eta\cdot \left( sign (\nabla E) + \rho \cdot W_{t-1} \right) + \mu \cdot \Delta W_{t-1} $$ где $$ sign(x) = \left\{\begin{array}{ r c c } -1 & : & x\lt 0 \\ 0 & : & x = 0 \\ 1 & : & x \gt 0 \end{array} \right. $$
7. Метод сопряжённых градиентов
В этом разделе мы рассмотрим метод сопряжённых градиентов (conjugate gradient). Особенность этого метода - специальный выбор направление изменения параметров. Оно выбирается таким образом, что бы было ортогональным к предыдущим направлениям. Полное изменение весов выглядит следующим образом. $$ \Delta W := \eta \cdot ( p + \rho \cdot W ) + \mu \cdot \Delta W $$ где $\eta$ - коэффициент скорости обучения,$p$ - направление изменения параметров,
$\mu$ - коэффициент момента,
$\Delta W$ - изменение весов на предыдущей итерации,
$\rho$ - коэффициент регуляризации,
$W$ - значения весов на предыдущей итерации.
При этом коэффициент скорости обучения $\eta$, выбирается на каждой итерации, путём решения задачи оптимизации. $$ \min_\eta E(\Delta W(\eta)) $$
Направление изменения параметров выбирается следующим образом. $$ p = \nabla E + \beta\cdot p $$ Начальное направление выбирается как $ p_0 := \nabla E $.
Ключевым моментом является вычисление коэффициента сопряжения $\beta$. Его можно вычислять по крайней мере двумя разными способами. Первый способ - формула Флетчера-Ривса. $$ \beta = \frac{g_t^T\cdot g_t}{g_{t-1}^T\cdot g_{t-1}}; $$ Второй способ - формула Полака-Рибьера. $$ \beta=\frac{g_t^T\cdot (g_t-g_{t-1})}{g_{t-1}^T\cdot g_{t-1}}; $$ где $g = \nabla E$ - градиент функции потери на этой и предыдущей итерациях.
Для компенсации накапливающейся погрешности вычислений метод предусматривает сброс сопряженного направления т.е. ($\beta:=0$, $p := \nabla E$) через каждые $n$ циклов, где $n$ выбирается в зависимости от количества параметров W.
8. Метод NAG (Nesterov’s Accelerated Gradient)
В этом разделе мы рассмотрим модификацию метода градиентного спуска NAG, здесь градиент вычисляется относительно сдвинутых на значение момента весов. $$ \Delta W_t := \eta\cdot \left( \nabla E( W_{t-1} + \mu \cdot \Delta W_{t-1} ) + \rho \cdot W_{t-1} \right) + \mu \cdot \Delta W_{t-1} $$ где $\eta$ - коэффициент скорости обучения,$\nabla E$ - градиент функции потери,
$\mu$ - коэффициент момента,
$\Delta W_{t-1}$ - изменение весов на предыдущей итерации,
$\rho$ - коэффициент регуляризации,
$W_{t-1}$ - значения весов на предыдущей итерации.
(I.Sutskever, J.Martens, G.Dahl, G.Hinton On the importance of initialization and momentum in deep learning)
9. Метод AdaGrad (Adaptive Gradient)
Метод AdaGrad учитывает историю значений градиента следующим образом. $$ g_t := \frac{ \nabla E_t } { \sqrt{ \sum\limits_{i=1}^t \nabla E_i^2 } } $$ $$ \Delta W_t := \eta\cdot \left( g_t + \rho \cdot W_{t-1} \right) + \mu \cdot \Delta W_{t-1} $$ где $\eta$ - коэффициент скорости обучения,$\nabla E$ - градиент функции потери,
$\mu$ - коэффициент момента,
$\Delta W_{t-1}$ - изменение весов на предыдущей итерации,
$\rho$ - коэффициент регуляризации,
$W_{t-1}$ - значения весов на предыдущей итерации.
(J.Duchi, E.Hazan, Y.Singer, Adaptive Subgradient Methods for Online Learning and Stochastic Optimization)
10. Метод AdaDelta
Метод AdaDelta учитывает историю значений градиента и историю изменения весов следующим образом. $$ S_t := \alpha \cdot S_{t-1} + (1-\alpha) \cdot \nabla E_t^2 \ ;\ S_0 := 0 $$ $$ D_t := \beta \cdot D_{t-1} + (1-\beta) \cdot \Delta W_{t-1}^2 \ ;\ D_0 := 0 $$ $$ g_t := \frac{ \sqrt{ D_t } } { \sqrt{ S_t } } \cdot \nabla E_t $$ $$ \Delta W_t := \eta\cdot \left( g_t + \rho \cdot W_{t-1} \right) + \mu \cdot \Delta W_{t-1} $$ где $\eta$ - коэффициент скорости обучения,$\nabla E$ - градиент функции потери,
$\mu$ - коэффициент момента,
$\Delta W_{t-1}$ - изменение весов на предыдущей итерации,
$\rho$ - коэффициент регуляризации,
$W_{t-1}$ - значения весов на предыдущей итерации,
$\alpha = \beta = 0.9$
(M.Zeiler Adadelta: an adaptive learning rate method)
11. Метод Adam
Метод Adam преобразует градиент следующим образом. $$ S_t := \alpha \cdot S_{t-1} + (1-\alpha) \cdot \nabla E_t^2 \ ;\ S_0 := 0 $$ $$ D_t := \beta \cdot D_{t-1} + (1-\beta) \cdot \nabla E_t \ ;\ D_0 := 0 $$ $$ g_t := \frac{ D_t }{1-\beta} \cdot \sqrt{ \frac{1-\alpha}{ S_t } } $$ $$ \Delta W_t := \eta\cdot \left( g_t + \rho \cdot W_{t-1} \right) + \mu \cdot \Delta W_{t-1} $$ где $\eta$ - коэффициент скорости обучения,$\nabla E$ - градиент функции потери,
$\mu$ - коэффициент момента,
$\Delta W_{t-1}$ - изменение весов на предыдущей итерации,
$\rho$ - коэффициент регуляризации,
$W_{t-1}$ - значения весов на предыдущей итерации,
$\alpha = 0.999,\ \beta = 0.9$
(Diederik P. Kingma, Jimmy Lei Ba Adam: a method for stochastic optimization)
12. Реализации.
В этом разделе мы представим реализации описанных выше методов. Тестировать их будем на нескольких наборах данных - три набора точек (в двух классах) и набор картинок с цифрами от 0 до 9 для распознавания. Каждый набор точек перед запуском процедуры обучения случайным образом делиться на три части: учебный, контрольный и тестовый.12.1 Первый набор.
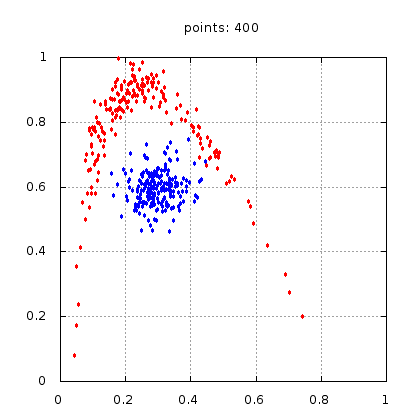
Рис.: учебный набор |

Рис.: контрольный набор |
Рис.: тестовый набор
Далее представим результаты для разных методов обучения.
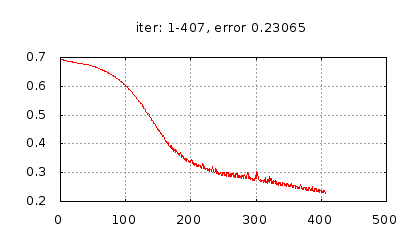
Рис.: история изменения ошибки ч.1
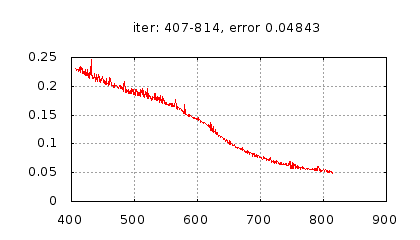
Рис.: история изменения ошибки ч.2 |
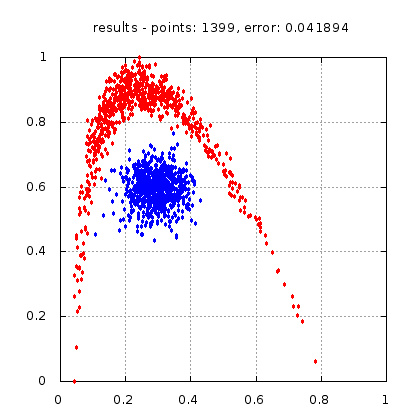
Рис.: результат теста |
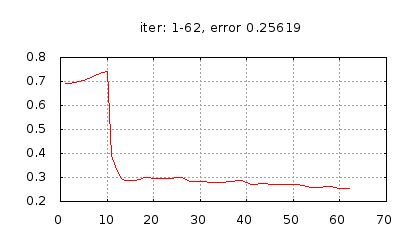
Рис.: история изменения ошибки ч.1
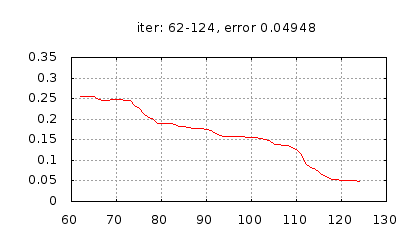
Рис.: история изменения ошибки ч.2 |
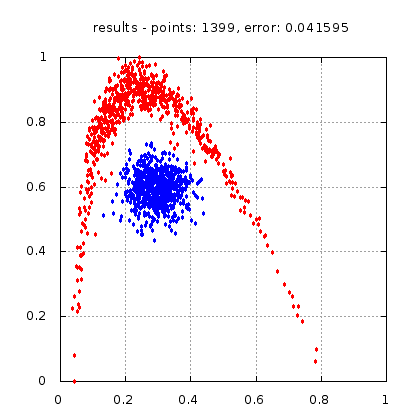
Рис.: результат теста |
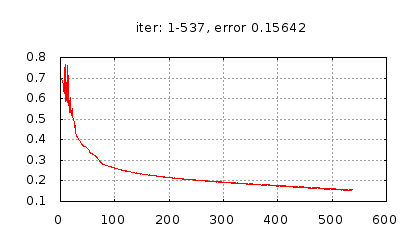
Рис.: история изменения ошибки ч.1
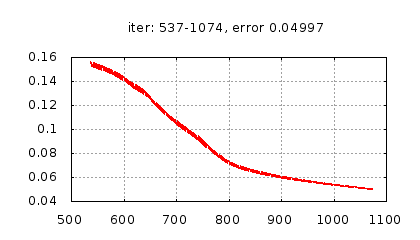
Рис.: история изменения ошибки ч.2 |
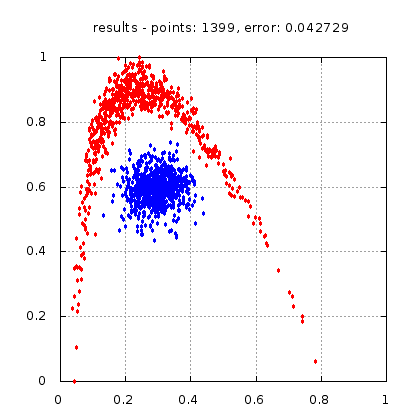
Рис.: результат теста |
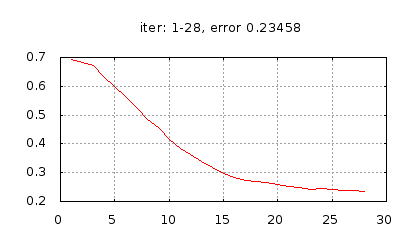
Рис.: история изменения ошибки ч.1
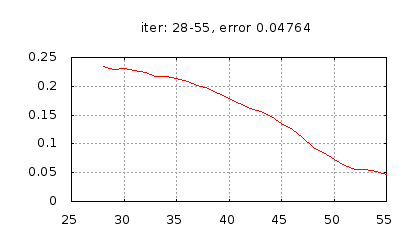
Рис.: история изменения ошибки ч.2 |
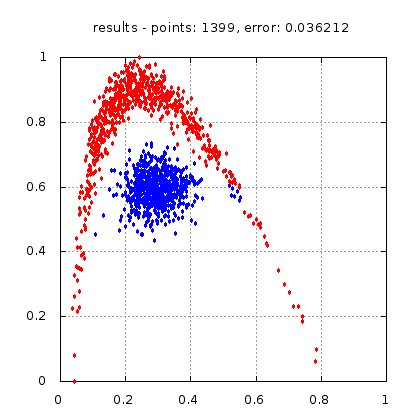
Рис.: результат теста |
12.2 Второй набор.
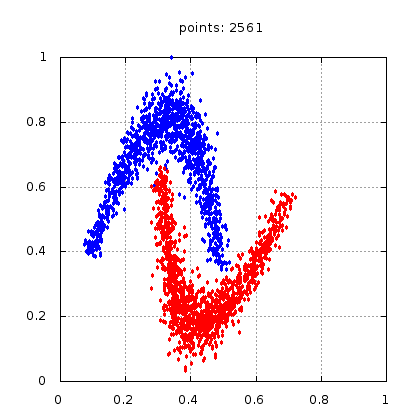
Рис.: учебный набор |
Рис.: контрольный набор |
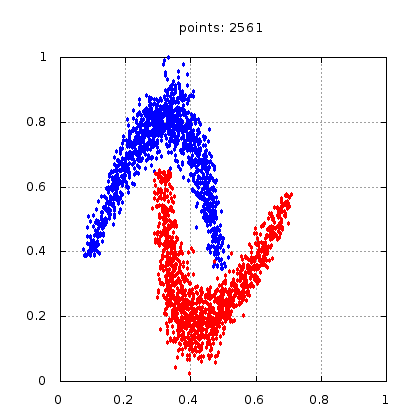
Рис.: тестовый набор
Далее представим результаты для разных методов обучения.
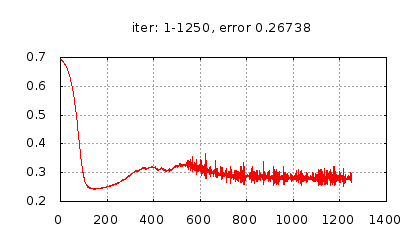
Рис.: история изменения ошибки ч.1
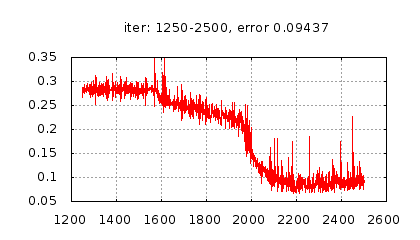
Рис.: история изменения ошибки ч.2 |
Рис.: результат теста |
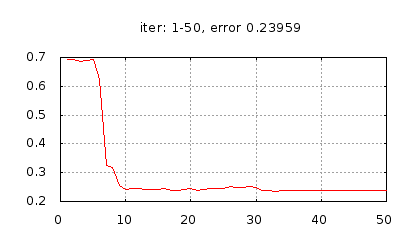
Рис.: история изменения ошибки ч.1
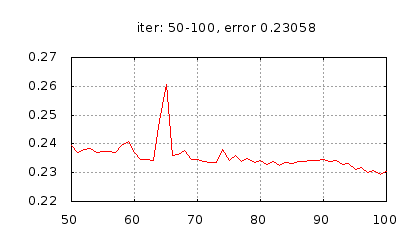
Рис.: история изменения ошибки ч.2 |
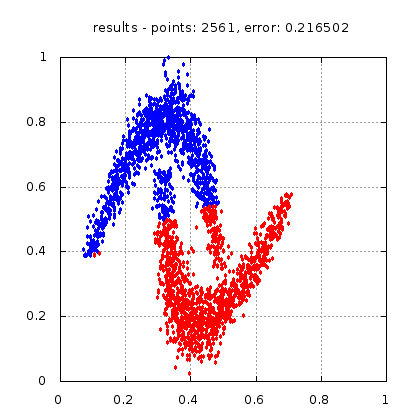
Рис.: результат теста |
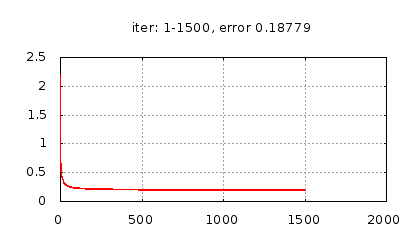
Рис.: история изменения ошибки ч.1
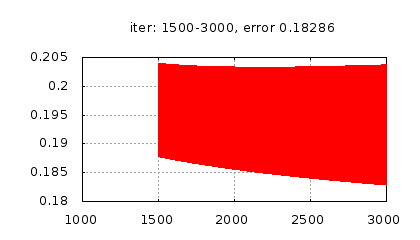
Рис.: история изменения ошибки ч.2 |
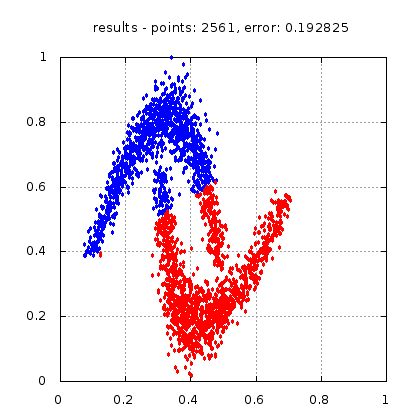
Рис.: результат теста |
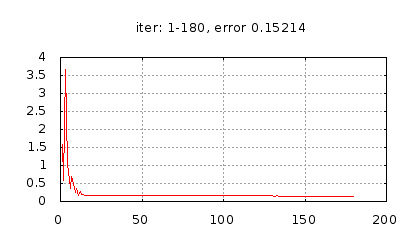
Рис.: история изменения ошибки ч.1
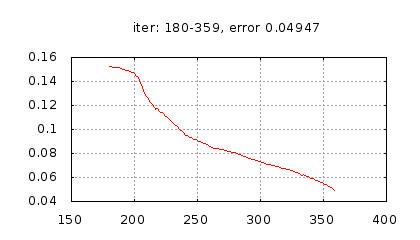
Рис.: история изменения ошибки ч.2 |
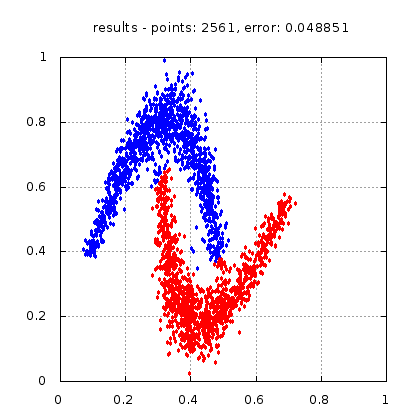
Рис.: результат теста |
12.3 Третий набор.
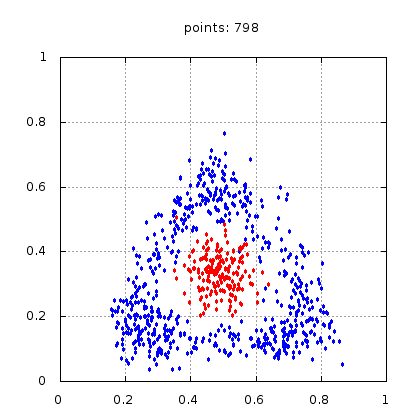
Рис.: учебный набор |

Рис.: контрольный набор |
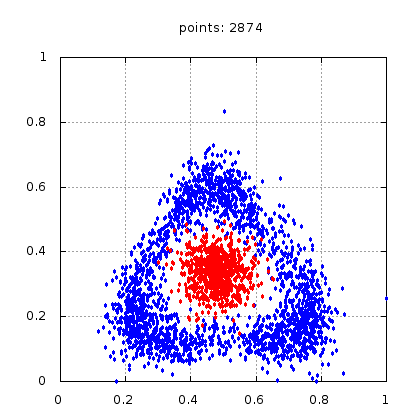
Рис.: тестовый набор
Далее представим результаты для разных методов обучения.
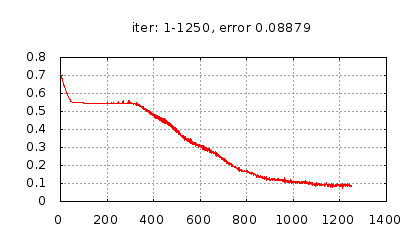
Рис.: история изменения ошибки ч.1
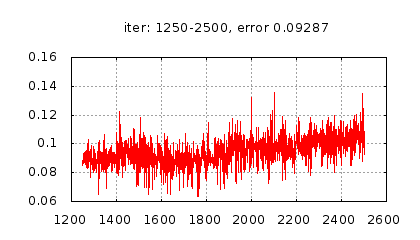
Рис.: история изменения ошибки ч.2 |
Рис.: результат теста |
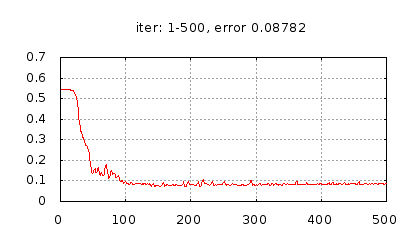
Рис.: история изменения ошибки ч.1
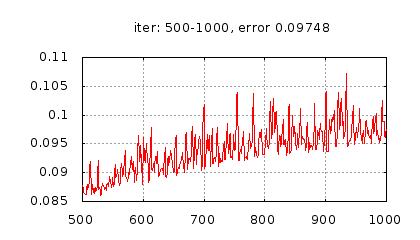
Рис.: история изменения ошибки ч.2 |
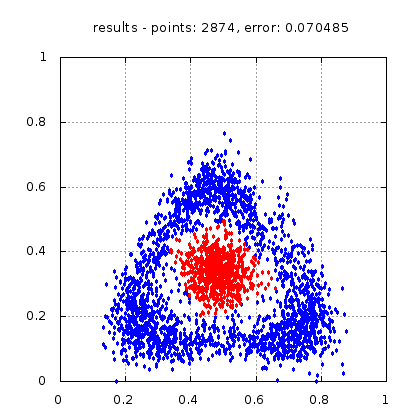
Рис.: результат теста |
|
Рис.: история изменения ошибки ч.1
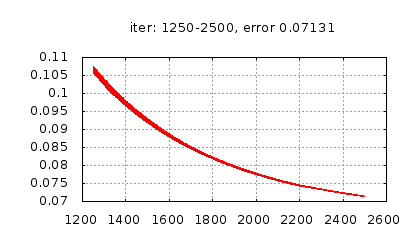
Рис.: история изменения ошибки ч.2 |
Рис.: результат теста |
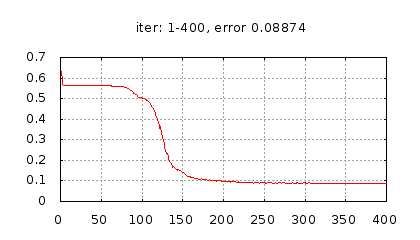
Рис.: история изменения ошибки ч.1
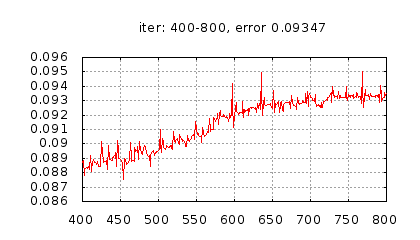
Рис.: история изменения ошибки ч.2 |
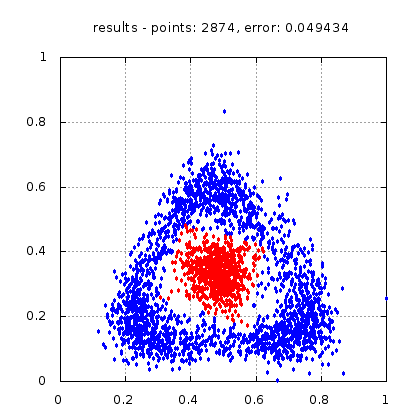
Рис.: результат теста |
12.4 Набор картинок.
| учебный набор: |

|

|

|

|

|

|

|

|

|

|
| тестовый набор: |

|

|

|

|

|

|

|

|

|
Далее представим результаты для разных методов обучения.

Рис.: история изменения ошибки ч.1 |

Рис.: история изменения ошибки ч.2 |



















































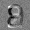






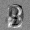






















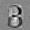
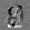

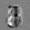

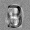

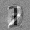
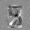







































Рис.: состояния весов первого слоя

Рис.: история изменения ошибки ч.1 |
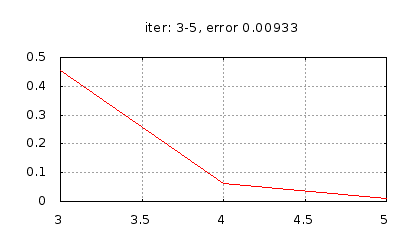
Рис.: история изменения ошибки ч.2 |











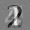
















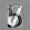





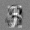


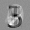







































































































Рис.: состояния весов первого слоя

Рис.: история изменения ошибки ч.1 |
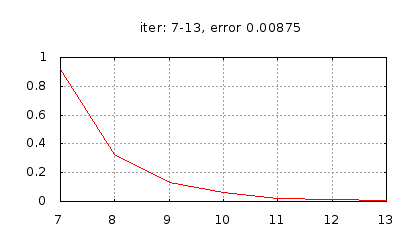
Рис.: история изменения ошибки ч.2 |


















































































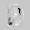












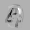

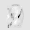










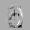






Рис.: состояния весов первого слоя

Рис.: история изменения ошибки ч.1 |
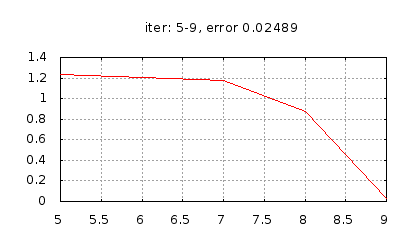
Рис.: история изменения ошибки ч.2 |
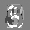
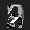
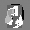
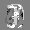
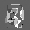
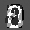
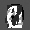
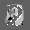
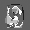
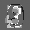
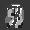
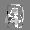
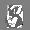
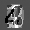
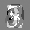
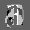
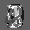
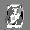
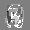
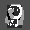

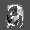
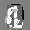
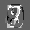
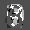

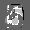
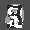
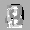
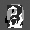
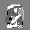
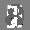
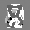
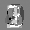
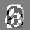
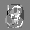
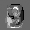
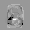
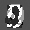
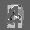
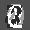
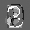
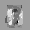
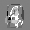
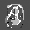
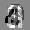
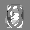
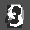
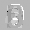
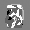
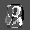
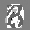
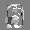
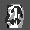
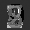
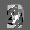
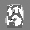
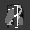
Рис.: состояния весов первого слоя
Список литературы
- Е.С.Борисов Основные модели и методы теории искусственных нейронных сетей. - http://www.mechanoid.kiev.ua
- Е.С.Борисов О методах обучения многослойных нейронных сетей прямого распространения. ч.1 Общие положения - http://www.mechanoid.kiev.ua
- Е.С.Борисов О методах обучения многослойных нейронных сетей прямого распространения. ч.3 Градиентные методы второго порядка - http://www.mechanoid.kiev.ua
- Осовский С. Нейронные сети для обработки информации. — М.: Финансы и статистика, 2002.
- GNU Octave -- http://www.gnu.org/software/octave
