Классификатор на основе нейронной сети Хемминга.

Е.С.Борисов

воскресенье, 23 октября 2005 г.

В этой работе построен классификатор распознающий картинки с цифрами от 0 до 9 . Для реализации классификатора используется нейронная сеть Хемминга.

1 Модель

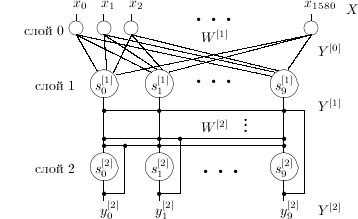
Искусственная нейронная сеть Хемминга (рис. 1 ) была предложена в 1987 г. Р. Липманом [ 1 , 2 ]. Она представляет собой сеть с двумя обрабатывающими слоями: первый слой - слой Хемминга, второй слой - немного изменённая сеть Хопфилда .

**Рисунок 1:** нейронная сеть Хемминга

На вход нейронной сети подаётся картинка в формате BMP , размером 17 x 31 точек, представляющая собой матрицу 51 x 31 байт, таким образом входной (или распределительный) слой сети (слой 0 на рис. 1 ) состоит из 51 x 31 = 1581 нейронов.

Размерность скрытого слоя ( слой 1 на рис. 1 ) определяется количеством идеальных образцов, хранимых сетью, т.е. 10 нейронов. Размерность выходного слоя ( слой 2 на рис. 1 ) равна размерности скрытого слоя нейронной сети, т.е. так же 10 нейронов.

На выходе получаем вектор y(y ₀ ...y ₉ ) . Номер j , для которого y _j ^[2] > 0 , соответствует номеру класса входного образца.

1.1 Параметры сети

Первый слой - слой Хемминга, представляет собой нейронную сеть с прямыми связями. Этот слой вычисляет меру подобия (расстояние Хемминга) между всеми эталонными образцами, хранящимися в сети, и текущим входом сети. Расстояние Хемминга это количество отличающихся компонент во входном и эталонном векторах.

Для этого слоя используется линейная функция активации ( y _i ^[1] = s _i ^[1] ). Состояние и выходное значение нейрона i слоя 1 определяется следующим образом:

$\begin{displaymath}y_i^{[1]}=s_i^{[1]}=\sum\limits_{j=0}^{1580} y_j^{[0]}\cdot w_{ij}^{[1]}\end{displaymath}$

где

y _i ^[1] - выходное значение нейрона i слоя 1;
s _i ^[1] - состояние нейрона i слоя 1;
y _j ^[0] - вход нейронной сети номер j ;
w _ij ^[1] - весовой коэффициент синаптической связи, соединяющей вход j нейронной сети и нейрон i слоя 1 ;

Второй слой это сеть Хопфилда , она используется для разрешения конфликтов, когда входной вектор оказывается похож по Хеммингу на более чем один идеал.

Начальное состояние нейронов слоя 2 определяется выходом первого слоя:

s _i ^[2] (0)= y _i ^[1]

Отношение переходов между состояниями нейронов слоя 2 определяется следующим образом:

$\begin{displaymath} s_i^{[2]}(t+1)=y_i^{[2]}(t) - c \cdot \sum\limits_{j\neq i} y_j^{[2]}(t) \end{displaymath}$

(1)

где

s _i ^[2] (t) - состояние нейрона i слоя 2 в момент времени t ;
y _i ^[2] (t) - выходное значение нейрона i слоя 2 в момент времени t ;
c - коэффициент торможения, 0< c < 0.1 ;

Легко видеть, что отношение переходов ( 1 ) эквивалентно обычному определению состояния нейрона (сумма взвешенных входов) с постоянной матрицей весов( 2 ).

$\begin{displaymath} w_{ij}^{[2]}= \left\{ \begin{array}{ccc} 1 &,& i=j \\ -c &,& i\neq j \end{array}\right. \end{displaymath}$

(2)

В качестве функции активации слоя 2 будем использовать следующую функцию :

1.2 Метод обучения

Весовые коэффициенты слоя 1 определяются следующим образом:

w _ji ^[1] =0.5 _* x _i ^j

(3)

где

w _ji ^[1] - весовой коэффициент синаптической связи, соединяющей вход i нейронной сети и нейрон j слоя 1 ;
x _i ^j - компонента номер i идеального (учебного) вектора номер j ;

Весовые коэффициенты слоя 2 фиксированы отношением переходов( 1 ).

Алгоритм обучения нейронной сети сводится к начальной инициализации матрицы весов слоя 1 по ( 3 ).

2 Реализация

В этом разделе представлена реализация, описанной выше модели классификатора, который работает с картинками в формате BMP.

На вход классификатора подаются картинки размером 17 x 31 точек, на выходе получаем - номер класса, к которому принадлежит входная картинка. Такой классификатор обладает хорошими способностями к обобщению, может корректно распознавать даже сильно искаженные и зашумленные картинки, к тому же, в отличии от классификатора на основе многослойной нейронной сети , он не требует идеальных выходных векторов и длительного процесса обучения. В программе используется библиотека для работы с картинками GdkPixbuf v.2 . Результат работы программы на рис. 2 .

Рисунок 2: Результат работы программы

ideal:
test:
output:	0	1	2	3	4	5	6	7	8	9

Исходные тексты программы [ здесь ].

Реализация в системе Octave [ здесь ].

Литература

1: Lipman R. An introdaction to computing with neural nets // IEEE Acoustic,Speech and Signal Processing Magazine,1987,no 2,L.4-22.
2: В.А.Головко, под ред.проф.А.И.Галушкина Нейронные сети: обучение, организация и применение. - Москва : ИПРЖР, 2001

Evgeny S. Borisov
2005-10-24

При использовании материалов этого сайта, пожалуйста вставляйте в свой текст ссылку на мою статью.