
[
на главную
]
О рекуррентных нейронных сетях
Евгений Борисовсреда, 29 марта 2017 г.
1. Введение
Существуют актуальные задачи обработки данных, при решении которых мы сталкиваемся не с отдельными объектами но с их последовательностями, т.е. порядок следования объектов играет существенную роль в задаче. Например, это задача распознавания речи, где мы имеем дело с последовательностями звуков или некоторые задачи обработки текстов на естественном языке [2], где мы имеем дело с последовательностями слов.Для решения такого рода задач можно применять рекуррентные нейронные сети, которые в процессе работы могут сохранять информацию о своих предыдущих состояниях. Далее мы рассмотрим принципы работы таких сетей на примере рекуррентной сети Элмана [1].
2. Схема работы рекуррентной нейронной сети
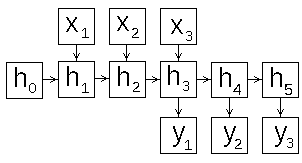
Искусственная нейронная сеть Элмана [1], известная так же как Simple Recurrent Neural Network, состоит из трех слоёв - входного (распределительного) слоя, скрытого и выходного (обрабатывающих) слоёв. При этом скрытый слой имеет обратную связь сам на себя. На рис.1 представлена схема нейронной сети Элмана.
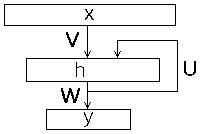
Рис 1: схема нейронной сети Элмана
В отличии от обычной сети прямого распространения [3], входной образ рекуррентной сети это не один вектор но последовательность векторов $\{x(1),\ldots x(n)\}$, векторы входного образа в заданном порядке подаются на вход, при этом новое состояние скрытого слоя зависит от его предыдущих состояний. Сеть Элмана можно описать следующими соотношениями. $$ h(t) = f \left( V\cdot x(t) + U\cdot h(t-1)+ b_h \right) $$ $$ y(t) = g \left(W \cdot h(t) + b_y \right) $$ здесь
$x(t)$ - входной вектор номер $t$,
$h(t)$ - состояние скрытого слоя для входа $x(t)$ ( $h(0) = 0$ ),
$y(t)$ - выход сети для входа $x(t)$,
$U$ - весовая матрица распределительного слоя,
$W$ - весовая (квадратная) матрица обратных связей скрытого слоя,
$b_h$ - вектор сдвигов скрытого слоя,
$V$ - весовая матрица выходного слоя,
$b_y$ - вектор сдвигов выходного слоя
$f$ - функция активации скрытого слоя
$g$ - функция активации выходного слоя
При этом возможны различные схемы работы сети, о которых мы поговорим в следующем разделе.
3. Схемы работы рекуррентной нейронной сети
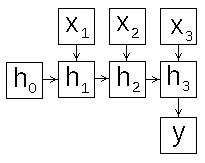
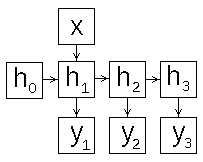
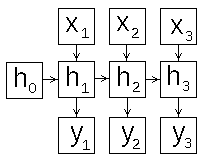
В зависимости от того как сформировать вход и выход рекуррентной сети, можно разными способами задать схему её работы. Рассмотрим этот вопрос подробнее, для этого развернём схему рекуррентной сети во времени (рис.2).
|
|
|
| a) | b) | c) |
|
| d) |
Рис 2: схемы работы рекуррентной нейронной сети
Перечислим возможные способы организации работы рекуррентной сети [4,5].
- "много в один" (many-to-one) рис.2a - скрытый слой последовательно изменяет своё состояние, из его конечного состояния вычисляется выход сети, эту схему можно использовать для классификации текстов ;
- "один во много" (one-to-many) рис.2b - скрытый слой инициализируется одним входом, из цепочки его последующих состояний генерируются выходы сети, эту схему можно использовать для аннотирования изображений ;
- "много во много" (many-to-many) рис.2c - на каждый вход сеть выдаёт выход, который зависит от предыдущих входов, эту схему можно использовать для классификации видео ;
- "много во много" (many-to-many) рис.2d - скрытый слой последовательно изменяет своё состояние, его конечное состояние служит инициализацией для выдачи цепочки результатов, эту схему можно использовать для создания систем машинного перевода и чат-ботов ;
Далее мы рассмотрим метод обучения сети Элмана.
4. Метод обучения рекуррентной нейронной сети (BPTT)
В этом разделе мы опишем метод обучения рекуррентной сети Элмана по схеме many-to-one (рис.2a), для реализации классификатора объектов, заданных последовательностями векторов. Для обучения сети Элмана применяются те же градиентные методы [3], что и для обычных сетей прямого распространения, но с определёнными модификациями для корректного вычисления градиента функции ошибки. Он вычисляется с помощью модифицированного метода обратного распространения [3], который носит название Backpropagation through time (метод обратного распространения с разворачиванием сети во времени, BPTT) [6]. Идея метода - развернуть последовательность, превратив рекуррентную сеть в "обычную" (рис.2a). Как и в методе обратного распространения для сетей прямого распространения [3], процесс вычисления градиента (изменения весов) происходит в три следующих этапа.- прямой проход - вычисляем состояния слоёв,
- обратный проход - вычисляем ошибку слоёв,
- вычисление изменения весов, на основе данных полученных на первом и втором этапах.
Рассмотрим эти этапы подробнее.
1. Прямой проход: для каждого вектора последовательности $\{x(1),\ldots x(n)\}$ :
вычисляем состояния скрытого слоя $\{s(1),\ldots s(n)\}$ и выходы скрытого слоя $\{h(1),\ldots h(n)\}$
$$ s(t) = V\cdot x(t)+U\cdot h(t-1)+ a $$ $$ h(t) = f \left( s(t) \right) $$ вычисляем выход сети $y$
$$ y(n) = g\left( W \cdot h(n) + b \right) $$
2. Обратный проход: вычисляем ошибку выходного слоя $\delta_o$
$$ \delta_o = y - d $$ вычисляем ошибку скрытого слоя в конечном состоянии $\delta_h(n)$
$$ \delta_h(n) = W^T \cdot \delta_o \odot f'(s(n)) $$ вычисляем ошибки скрытого слоя в промежуточных состояниях $\delta_h(t)$ ($t=1,\ldots n$)
$$ \delta_h(t) = U^T \cdot \delta_h(t+1) \odot f'(s(n)) $$
3. Вычисляем изменение весов: $$ \Delta W = \delta_o \cdot (h(n))^T $$ $$ \Delta b_y = \sum \delta_o $$ $$ \Delta V = \sum_t \delta_h(t) \cdot (x(t))^T $$ $$ \Delta U = \sum_t \delta_h(t) \cdot (h(t-1))^T $$ $$ \Delta b_h = \sum\sum_t \delta_h(t) $$
Найдя способ вычисления градиента функции ошибки, далее мы можем применить одну из модификаций метода градиентного спуска, которые подробно описаны в [3].
5. Реализация
В этом разделе представлена реализация рекуррентной сети Элмана по схеме many-to-one (рис.2a), активация скрытого слоя - гиберболический тангенс (tanh), активация выходного слоя (softmax), функция ошибки - средняя кросс-энтропия. Учебные данные генерируются случайным образом.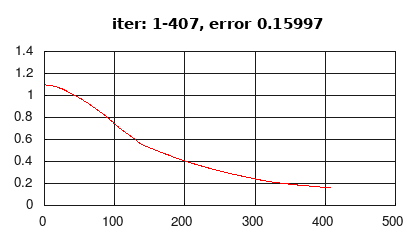
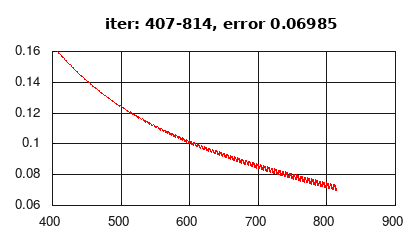
Рис 3: история изменения ошибки обучения
Полный текст на octave можно скачать [ здесь ].
Литература
- Jeffrey L. Elman Finding Structure in Time // COGNITIVE SCIENCE 14, 179-211 (1990)
-
Е.С.Борисов Классификатор текстов на естественном языке.
- http://www.mechanoid.kiev.ua/neural-net-classifier-text.html -
Е.С.Борисов О методах обучения многослойных нейронных сетей прямого распространения.
- http://www.mechanoid.kiev.ua/neural-net-backprop.html -
Andrej Karpathy The Unreasonable Effectiveness of Recurrent Neural Networks
- http://karpathy.github.io/2015/05/21/rnn-effectiveness/ -
Павел Нестеров Рекуррентные нейронные сети
- https://www.youtube.com/watch?v=KPT8akr3udk -
Werbos, P. J. Backpropagation through time: what it does and how to do it.
- Proc. IEEE, 1990 78(10):1550-1560.
