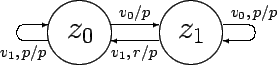Многомашинный вычислительный комплекс.

Евгений Борисов

21 октября 2000 г.

1 Введение

Возможности наращивания производительности ЭВМ путем повышения скорости работы процессора в настоящее время приближаются к пределу и связаны с существенным увеличением стоимости аппаратуры. Большие возможности и резервы открываются в использовании многопроцессорных архитектур. При одинаковой потенциальной производительности система с большим числом процессоров может обладать большей гибкостью, допуская различные формы организации вычислительных процессов. Необходимо отметить, что такие системы требуют специальных операционных систем.
Многопроцессорные системы могут быть классифицированы в зависимости оттого, как решаются три основные проблемы, определяющие их организацию : управление, память и связь.

1.1 Управление

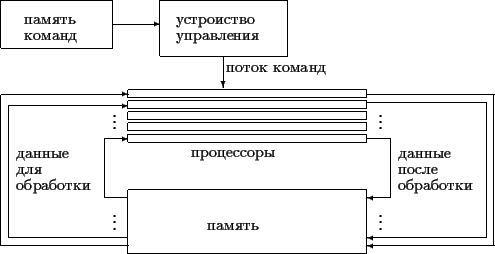
Проблема управления - имеет два основных решения: централизованное и распределённое, что соответствует системам типа SIMD и MIMD по известной классификаций Флинна.

SIMD "single instruction multiple data" (один поток команд много потоков данных), команды выдаются управляющим модулем и выполняются одновременно на всех процессорах системы.

Рисунок 1: схема SIMD
$\begin{figure}\centering \begin{picture}(310,160) % put(0,0)\{ rectangle\{310\}... ... \put(20,45){после} \put(20,35){обработки} } \end{picture}\par\end{figure}$
MIMD "multiple instruction multiple data" (много потоков команд много потоков данных), связная совокупность процессоров, работающих по своим программам и со своими исходными данными.

Рисунок 2: схема MIMD
$\begin{figure}\centering \begin{picture}(320,115) % put(0,0)\{ rectangle\{320\}... ... \put(20,45){после} \put(20,35){обработки} } \end{picture}\par\end{figure}$

**Рисунок 1:** схема SIMD
$\begin{figure}\centering \begin{picture}(310,160) % put(0,0)\{ rectangle\{310\}... ... \put(20,45){после} \put(20,35){обработки} } \end{picture}\par\end{figure}$

**Рисунок 2:** схема MIMD
$\begin{figure}\centering \begin{picture}(320,115) % put(0,0)\{ rectangle\{320\}... ... \put(20,45){после} \put(20,35){обработки} } \end{picture}\par\end{figure}$

1.2 Память

В системах с общей памятью требуется специальная аппаратура для разрешения конфликтов и достаточно сложное коммутационное оборудование. Сложность таких систем растет пропорционально квадрату числа процессоров.
Применение распределенной памяти означает, что каждый процессор имеет свою собственную оперативную память, объем которой достаточно велик для самостоятельного выполнения отдельных заданий.

1.3 Связь

Связь между процессорами представляет собой наиболее сложную проблему и имеет много решений. Удобно различать универсальные и специальные системы связи.

Универсальная связь позволяет осуществлять любые парные соединения процессоров (каждый с каждым). Универсальная связь технически может быть реализована либо с помощью общей шины, либо с помощью коммутационной системы.
В специальных системах связи каждый процессор может непосредственно связываться лишь с ограниченным множеством других процессоров. Процессоры в таких системах образуют сеть, которая может иметь самую разнообразную топологию : двумерная или трехмерная решетка, древообразные сети и др.

2 Постановка задачи

Вычислительные системы сверхвысокой производительности стоят дорого. Но существует возможность объединить мощности нескольких PC для решения задач, требующих большой вычислительной мощности. В данной работе предлагается "дешевый суперкомпьютер". На аппаратной базе локальной сети строиться распределенная многопроцессорная система - мы объединяем несколько компьютеров в виртуальную многопроцессорную машину. Ниже предлагается автоматная модель и пример реализации такой виртуальной машины.

**Рисунок 3:** виртуальная многопроцессорная машина
$\begin{figure}\centering \begin{picture}(170,135) % put(0,0)\{ rectangle\{170\}... ...t(80,35){\vector(0,-1){20}} \put(60,7){результат} \end{picture}\end{figure}$

3 Описание модели

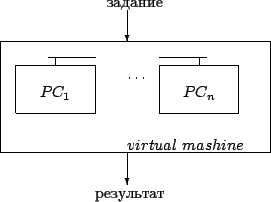
Предлагаемая модель состоит из автоматов двух типов:

**Рисунок 4:** схема модели

где

X -- множество входов системы
S -- управляющий модуль
D -- множество выходов на вычислительные модули
M _i -- i -тый вычислительный модуль
Y -- множество выходов системы

3.1 Вычислительный модуль

M = ( Z, V, R, α,β, z ₀ )

**Рисунок 5:** автомат-вычислитель
$\begin{figure}\centering \begin{picture}(180,40) % put(0,0)\{ rectangle\{180\}\... .../p$} \put(75,30){$v_0/p$} \put(70,5){$v_1,r/p$} \end{picture}\end{figure}$

Z = { z ₀ , z ₁ } - множество состояний;
- z ₀ - ожидание задания (начальное состояние );
- z ₁ - обработка задания и выдача результата;
V = { v ₀ ,v ₁ ,p } - множество входов;
- v ₀ - задание;
- v ₁ - запрос результата;
- p - "пустое" слово;
R = { r, p } - множество выходов;
- r - результат;
- p - "пустое" слово;

α : Z × V → Z - функция переходов

	v ₀	v ₁	p
z ₀	z ₁	z ₀	z ₀
z ₁	z ₁	z ₀	z ₁

β : Z × V → R - функция выходов

	v ₀	v ₁	p
z ₀	p	p	p
z ₁	p	r	p

3.2 Управляющий модуль

S = ( Q, X, D, f, g, Y, q ₀ )

**Рисунок 6:** управляющий автомат

Q = Z ⁿ - множество состояний системы, n - количество вычислительных модулей. q ∈ Q - представляет собой вектор, где q _i - есть состояние i -того вычислительного модуля.
q ₀ - начальное состояние
X = { v ₀ ,v ₁ } - множество входов системы (X ⊂ V)
- v ₀ - задание
- v ₁ - выдача результата ( конец работы )
D = V ⁿ - множество выходов на вычислительные модули

f : Q × X → Q - функция переходов

	v ₀	v ₁
(z ₀ ,...,z ₀ )	(z ₁ ,z ₀ ,...,z ₀ )	(z ₀ ,...,z ₀ )
(z ₁ ,z ₀ ,...,z ₀ )	(z ₁ ,z ₁ ,z ₀ ,...,z ₀ )	(z ₀ ,...,z ₀ )
...	...	...
(z ₁ ,...,z ₁ ,z ₀ )	(z ₁ ,...,z ₁ )	(z ₀ ,...,z ₀ )
(z ₁ ,...,z ₁ )	(z ₀ ,...,z ₀ )	(z ₀ ,...,z ₀ )

g : Q × X → D - функция выходов на вычислительные модули

	v ₀	v ₁
(z ₀ ,...,z ₀ )	(v ₀ ,p,...,p)	(v ₁ ,...,v ₁ )
(z ₁ ,z ₀ ,...,z ₀ )	(p,v ₀ ,p,...,p)	(v ₁ ,...,v ₁ )
...	...	...
(z ₁ ,...,z ₁ ,z ₀ )	(p,...,p,v ₀ )	(v ₁ ,...,v ₁ )
(z ₁ ,...,z ₁ )	(v ₁ ,...,v ₁ )	(v ₁ ,...,v ₁ )

Отдаем задание первому свободному вычислительному модулю. Если свободных нет, то ждем освобождения ресурсов (собираем результаты). v ₁ на вход - конец работы (собираем результаты).

4 Реализация

Для прогона контрольных примеров была использована LAN Ethernet ( TCP/IP ) из двух машин Intel 486 DX2 50MHz .
Программы были написаны согласно выше изложенной автоматной модели на C++ под ОС QNX v.4.25 и Linux RED HAT 6 .
IP - адреса, или NetBEIU имена задействованных компьютеров содержатся в специальных конфигурационных файлах.
Количество подключаемых компьютеров может быть как угодно большим.
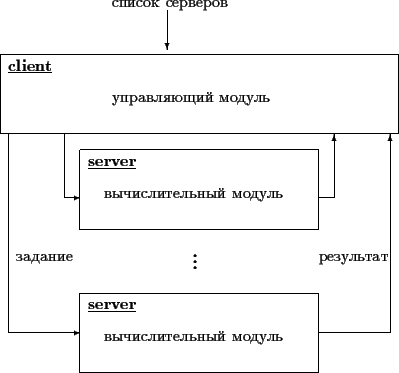
Клиент раздает задания серверам и собирает результаты счета. Таким образом происходит распараллеливание вычислительного процесса.
Прирост производительности двух процессорной VM по сравнению с одно процессорной при прогоне контрольных примеров составил 92% .

**Рисунок 7:** схема программной реализации
$\begin{figure}\centering \begin{picture}(250,245) % put(0,0)\{ rectangle\{250\}... ...ераций\} % put(195,228)\{ vector(0,-1)\{25\}\} \end{picture}\par\end{figure}$

4.1 Взломщик шифра

В этой работе предлагается простая система шифрования данных, которую можно отнести к классу симметричных криптосистем, и ''взломщик'' шифра. Процедура шифрования заключается в сложении по модулю 2 побайтно закрываемого текста и заданного пользователем ключа. Вскрытие кода осуществляется последовательным подбором ключа. Таким образом, количество необходимых для вскрытия итераций равно 2 ⁿ , где n - размерность ключа. Например, при n = 24 (трехбуквенный ключ) необходимо произвести 16777216 итераций. Ключ такой длинны был использован при контрольных прогонах программы.

server - реализует вычислительный модуль.

# serv

-= crypt sever v.2 =-

(c) Borisov E.S. Kiev UA
usage: serv <params>
params:
-p <server port> (default 5041)
-w <wordlist file>

close ..... ok

# serv -w data/test.lex

-= crypt sever v.2 =-

create ......... ok (port 5041)
wordlist 'data/test.lex'-14 words readed
accept ..... ok
disconnect ........ ok
close ......... ok

#_

client - реализует управляющий модуль.

# cl

-= crypt client v.2 =-

(c) Borisov E.S. Kiev UA
usage: cl <params>
params:
-c <config file>
-f <cryptogram file>
-k <max key length>

disconnect .... ok

#_

4.1.1 Результаты счета

Одна машина

Время счета - 318 секунд;

# cl -k3

-= crypt client v.2 =-

-----------
localhost:5041
-----------
create connection (localhost:5041) ... ok
disconnect .... ok
create connection (localhost:5041) ... ok
disconnect .... ok
-----------
time = 318 sec.
RESULT : key="REX"
disconnect .... ok

#_

Две машины

Время счета - 160 секунд;

# cl -k3

-= crypt client v.2 =-

-----------
localhost : 5041
qnx_1 : 5041
-----------
create connection (localhost : 5041) ... ok
disconnect .... ok
create connection (qnx_1 : 5041) ... ok
disconnect .... ok
create connection (localhost : 5041) ... ok
disconnect .... ok
create connection (qnx_1 : 5041) ... ok
disconnect .... ok
-----------
time = 160 sec.
RESULT : key = "REX"
disconnect .... ok

#_

4.2 Вычисление числа $\pi$

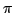
Число $\pi$ будем вычислять как определенный интеграл :

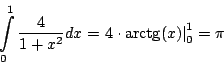
$\begin{displaymath}\int\limits_{0}^{1}{\frac{4}{1+x^2}}dx = \left. 4\cdot \arctg(x)\right\vert _0^1 = \pi\end{displaymath}$

Согласно правилу прямоугольников интеграл можно заменить суммой:

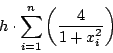
$\begin{displaymath}h \cdot \sum\limits_{i=1}^{n}\left(\frac{4}{1+x_i^2}\right)\end{displaymath}$

где h = 1/n ; x _i = ( i - 0.5 ) ^. h

server - реализует вычислительный модуль.

# pi.serv -?

 -=  PI calculation server (TCP) v.1 =-

  (c) Borisov E.S. Kiev UA
 usage: pi.serv <params> 
  params:
	 -p <server port number> (def.5041)
	 -w - write more information

# pi.serv

-=  PI calculation server (TCP) v.1 =-

create ........ ok  (port 5041)
accept ........ ok
disconnect .... ok
close ......... ok
#_

client - реализует управляющий модуль.

 
# pi.cl

-=  PI calculation client (TCP) v.1 =-

(c) Borisov E.S. Kiev UA
usage: pi.cl <params>
params:
-h <server name> - shutdown server
-p <server port number> (def. 5041)
-i <size of interval>

# pi.cl -h localhost

-=  PI calculation client (TCP) v.1 =-

connect to localhost:5041 ... ok
disconnect .................. ok

#_

pi.hosts - файл со списком серверов.
```
# PI servers 
localhost: 5041 
qnx_1    : 5041
```

4.2.1 Результаты счета

Одна машина

Количество итераций 10 ⁷
Время счета - 69 секунд
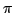$\pi$ = 3.141592753589926

# pi.cl -i20000000

-=  PI calculation client (TCP) v.1 =-

------ PI servers --------
qnx_1:5041
--------------------------
connect to qnx_1:5041 ... ok
disconnect .............. ok
connect to qnx_1:5041 ... ok
disconnect .............. ok
-------------------------
time = 69 sec.
pi=3.141592753589926
#_

Две машины

Количество итераций 10 ⁷
Время счета - 36 секунд
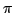$\pi$ = 3.141592753589926

# pi.cl -i20000000

-=  PI calculation client (TCP) v.1 =-

------ PI servers --------
qnx_1:5041
localhost:5041
--------------------------
connect to qnx_1:5041 ....... ok
disconnect .................. ok
connect to localhost:5041 ... ok
disconnect .................. ok
connect to qnx_1:5041 ....... ok
disconnect .................. ok
connect to localhost:5041 ... ok
disconnect .................. ok
--------------------------
time = 36 sec.
pi=3.141592753589926
#_

Исходные тексты программ

взломщик шифра [ QNX ]
вычисление числа 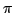$\pi$ [ QNX ] [ linux, FreeBSD ]

Литература

1: Ю.В.Капитонова, А.А.Летичевский ''Математическая теория проектирования вычислительных систем'' Москва,''Наука'',1988.
2: В.С.Михайлевич, Ю.В.Капитонова, А.А.Летичевский, И.Н.Молчанов,С.Б.Погребинский ''Организация вычислений в многопроцессорных вычислительных системах'' Кибернетика N3 1984.
3: В.С.Михайлевич,Ю.В.Капитонова, А.А.Летичевский ''О методах организации макроконвеерных вычислений'' Кибернетика N3 1986.
4: А.Е.Дорошенко ''Математические модели и методы организации высокопроизводительных параллельных вычислений'' Киев,''Наукова думка'',2000
5: В.В.Корнеев ''Параллельные вычислительные системы'' Москва,''Нолидж'',1999.
6: С.Баричев ''Криптография без секретов''.
7: А.Робачевский ''Операционная система UNIX'' Санкт-Петербург, ''bhv'', 1999.
8: Т.Чан ''Системное программирование на C++ для UNIX'' Киев, ''bhv'', 1999.
9: А.Колин ''Введение в операционные системы'' , Москва ''Мир'' 1975.
10: ''Программирование на параллельных вычислительных системах'' под ред. Р.Бэбба II Москва, ''Мир'', 1991.

Evgeny S. Borisov
2005-03-15

При использовании материалов этого сайта, пожалуйста вставляйте в свой текст ссылку на мою статью.