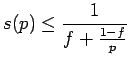Автоматизированная система декомпозиции последовательных программ для параллельных вычислителей с распределенной памятью.
Е.С.Борисов
четверг, 9 сентября 2004 г.
1 Введение
Существуют задачи, не решаемые на серийных персональных компьютерах за приемлемое время, к примеру прогнозирование погоды, моделирование процессов разрушения в механике (crash-тесты)[ 1 ]. Для решения таких задач используют многопроцессорные (параллельные) вычислители. Множество архитектур параллельных вычислителей весьма обширно. Основной характеристикой при классификации [ 2 ] параллельных вычислительных систем является способ организации памяти :
- общая память - все процессора работают в едином адресном пространстве с равноправным доступом к памяти
- распределенная память - каждый процессор имеет собственную локальную памятью, и прямой доступ к этой памяти других процессоров невозможен.
Для параллельных вычислительных систем необходимо создавать специальные программы. В тексте такой программы определяются части (ветки), которые могут выполнятся параллельно, а также алгоритм их взаимодействия.
Основным параметром оценки работы параллельной системы является коэффициент ускорения [ 4 ] :
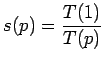
|
(1) |
где
Эффективность выполнения программы на параллельном вычислителе, в первую очередь, зависит от меры распараллеливания самой задачи, описываемой программой. Параллельные программы, вообще говоря, являются архитектурно зависимыми.
Оценить максимально возможное ускорение для данной программы можно, используя закон Амдала [ 3 ] :
где
2 Средства параллельных вычислений
Приведем краткое описание технологий параллельных вычислений. Средства параллельных вычислений можно разделить на три уровня :
2.1 Аппаратные средства для параллельных вычислений
Выделяют следующие классы параллельных систем.
-
SMP
- симметричная мультипроцессорная система. SMP обычно
состоит из нескольких одинаковых процессоров и массива
общей
памяти
. Все процессоры имеют доступ к любой точке памяти с одинаковой
скоростью. Наличие общей памяти упрощает взаимодействие процессоров
между собой, однако накладывает сильные ограничения на их число (обычно
не более 32).
-
PVP
- параллельная векторная система. Основным признаком
PVP-систем является наличие специальных векторно-конвейерных процессоров.
Как правило, несколько таких процессоров работают одновременно над
общей памятью (аналогично SMP) в рамках многопроцессорных конфигураций.
-
MPP
- система массового параллелизма. MPP состоит из
нескольких однородных вычислительных узлов. Каждый такой узел имеет
свою локальную память
(прямой доступ к памяти других узлов
невозможен), один или несколько центральных процессоров( иногда -
жесткий диск). Узлы обычно связаны специальной высокоскоростной сетью.
Общее число процессоров в таких системах может достигать нескольких
тысяч.
-
NUMA
- система с неоднородным
доступом к памяти. NUMA представляет собой нечто среднее между SMP и
MPP. В NUMA память физически распределена, но логически общедоступна.
Масштабируемость NUMA-систем ограничивается объемом адресного
пространства и возможностями операционной системы.
-
Кластеры
- недорогой вариант MPP. Обычно это сеть из
персональных компьютеров или рабочих станций общего назначения, которая
объединяется в
''виртуальную многопроцессорную машину''
. Для
связи узлов используется одна из стандартных сетевых технологий
(Ethernet, Myrinet).
2.2 Коммуникационные библиотеки
При написании параллельных программ можно пользоваться коммуникационными библиотеками. Такие библиотеки реализуют методы запуска и управления параллельными процессами, обычно они содержат функции обмена данными между ветвями параллельной программы, функции синхронизации процессов.
Соответственно типу организации памяти, существует два основных типа коммуникационных библиотек [ 5 ] и интерфейсов параллельного программирования :
- Библиотеки использующие модель общей памяти - этот класс библиотек обычно применяют для SMP систем
- Библиотеки построенные по модели обмена сообщениями удобно использовать для систем с распределенной памятью - массово-параллельные (MPP) и кластерные системы
Надо отметить, что одно может быть сымитировано через другое :
- модель обмена сообщениями для SMP - вырожденным каналом связи передачи сообщений служит разделяемая память.
- модель общей памяти для MPP - организация единого виртуального адресного пространства ( аппаратно реализовано на NUMA-машинах)
Существует множество библиотек и интерфейсов параллельного программирования. Отметим наиболее популярные из них.
-
OpenMP
(http://www.openmp.org) - программный интерфейс для
программирования компьютеров с общей памятью, т.е. для вычислителей
принадлежащих к классу симметричных мультипроцессоров (SMP) и к классу
систем с неоднородным доступом к памяти (NUMA).
-
PVM : parallel virtual machine
(http://www.epm.ornl.gov/pvm)
Эта система ориентирована на работу с гетерогенными кластерами, поддерживает
языки программирования C/C++/fortran, работает на широком классе систем,
включая рабочие станции, суперкомпьютеры и сети персональных компьютеров.
PVM реализует модели обмена сообщениями и динамического распараллеливания,
т.е. существует возможность порождать новые ветви параллельной программы
в процессе ее выполнения.
- MPI : Message Passing Interface (http://www.mpi-forum.org) - стандарт для построения параллельных программ по модели обмена сообщениями. Существуют реализации почти для всех суперкомпьютерных платформ, а также для сетей рабочих станций UNIX и Windows NT. Это наиболее популярный и широко используемый стандарт .
2.3 Средства автоматического распараллеливания
Параллельные программы можно писать ''вручную'', непосредственно вставляя в нужные места вызовы коммуникационной библиотеки. Этот путь требует от программиста специальной подготовки. Альтернативой является использование систем автоматического и полуавтоматического распараллеливания последовательных программ.
-
В случае
полуавтоматической системы распараллеливания
, в
тексте последовательной программы выделяются блоки, которые могут
выполнятся параллельно. Обычно, в текст вставляются специального
вида комментарии, которые игнорируются обычным (последовательным)
компилятором. Примером такой полуавтоматической системы может служить
Adaptor - одна из реализаций спецификации HPF : High Performance
Fortran (http://www.crpc.rice.edu/HPFF).
-
Автоматические системы распараллеливания
[
6
]
выполняют декомпозицию последовательного алгоритма самостоятельно.
На вход подается последовательная программа, на выход выдается её
параллельный аналог. Пример такой системы: BERT77 - средство
автоматического распараллеливания Fortran-программ
(http://www.plogic.com/bert.html). Системы из этого класса так же могут помочь пользователю выяснить, можно ли распараллелить данную задачу, оценить время ее выполнения, определить оптимальное число процессоров.
3 Математические модели
Рассмотрим три модели для описания параллельных вычислений. В этой работе применяется алгебродинамический подход к построению математических моделей параллельных вычислений[ 4 ]. Этот подход основывается на алгебре алгоритмов Глушкова[ 7 ]. Для описания функционирования моделей будем использовать понятия теории дискретных динамических систем[ 7 ].Дискретная динамическая система (ДДС, transition systems) представляет собой тройку :
где
-
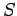 - множество состояний
- множество состояний
-
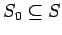 - множество начальных состояний
- множество начальных состояний
-
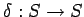 - отношения переходов
- отношения переходов
Алгебра алгоритмов Глушкова [ 7 ] определяется следующим образом. Введем три множества :
-
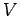 - множество переменных (память)
- множество переменных (память)
-
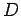 - множество значений переменных (данные)
- множество значений переменных (данные)
- - множество частичных отображений, его можно рассматривать как состояния памяти или информационную среду
Алгеброй алгоритмов назовем пару :
где
-
- алгебра операторов
-
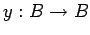 - множество частичных преобразований информационной среды
- множество частичных преобразований информационной среды
-
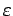 - тождественный оператор
- тождественный оператор
-
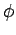 - пустой оператор
- пустой оператор
-
-
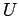 - алгебра условий
- алгебра условий
- 0 - тождественно ложное условие
-
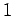 - тождественно истинное условие
- тождественно истинное условие
-
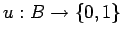 - множество частичных предикатов на
- множество частичных предикатов на
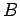
В алгебре алгоритмов ( 3 ) определены следующие операции :
-
последовательная композиция
операторов :
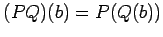
где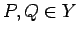 - операторы,
- операторы,
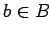 - состояние памяти
- состояние памяти
-
условный переход
:
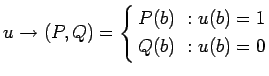
где
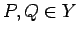 - операторы,
- операторы,
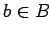 - состояние памяти,
- состояние памяти,
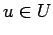 - условие
- условие
-
итерация
:
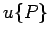
если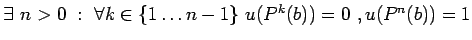
то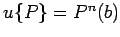
иначе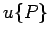 не определено
не определено
где
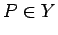 - оператор,
- оператор,
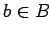 - состояние памяти,
- состояние памяти,
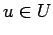 - условие
- условие
-
умножение оператора на условие
:
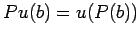
где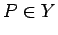 - оператор,
- оператор,
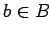 - состояние памяти,
- состояние памяти,
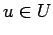 - условие
- условие
В алгебре операторов
выделяется множество базовых операторов, а в
алгебре условий
![]() выделяется множество базовых условий. Таким образом,
порождается алгебра алгоритмов
выделяется множество базовых условий. Таким образом,
порождается алгебра алгоритмов
![]() .
.
Регулярное выражение в
![]() назовём
регулярной программой
.
назовём
регулярной программой
.
Модели памяти
Для множества регулярных программ-
Множество переменных
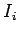 регулярной программы
регулярной программы
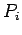 назовём множеством
внутренних переменных
или
внутренней памятью
программы
назовём множеством
внутренних переменных
или
внутренней памятью
программы
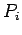 если
если
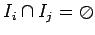 для
для
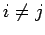
тогда множество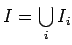 назовём
распределённой
памятью
назовём
распределённой
памятью
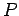
-
Все множество переменных
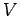 регулярной программы
регулярной программы
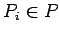 назовём
двухуровневой памятью
назовём
двухуровневой памятью
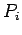
если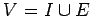 ;
;
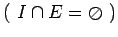 и определены
операторы внешнего обмена
-
чтение
и определены
операторы внешнего обмена
-
чтение
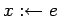 и запись
и запись
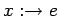 (
(
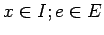 )
)
В этом случае,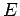 назовём
внешней памятью
назовём
внешней памятью
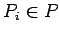
4 Постановка задачи и ее решение
Сформулируем постановку задачи: построить полуавтоматическую систему распараллеливания последовательных программ для параллельных вычислителей с распределенной памятью.
4.1 Модель полуавтоматической системы распараллеливания
Система полуавтоматического распараллеливания описывается тремя алгебродинамическими моделями :
-
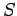 - модель исходной последовательной программы, состоящей из
определенного множества подпрограмм.
- модель исходной последовательной программы, состоящей из
определенного множества подпрограмм.
-
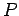 - модель параллельной программы. Данная модель построена на
основе парадигмы обмена сообщениями, и описывает статическое распараллеливание,
т.е. количество компонент параллельной программы фиксировано.
- модель параллельной программы. Данная модель построена на
основе парадигмы обмена сообщениями, и описывает статическое распараллеливание,
т.е. количество компонент параллельной программы фиксировано.
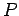 ориентирована на системы с распределенной памятью, без общей внешней
памяти (например - кластер на основе сети персональных компьютеров).
ориентирована на системы с распределенной памятью, без общей внешней
памяти (например - кластер на основе сети персональных компьютеров).
-
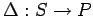 - модель транслятора-распараллеливателя на
основе дискретной динамической системы,
- модель транслятора-распараллеливателя на
основе дискретной динамической системы,
В основе, представленной ниже, системы полуавтоматического распараллеливания
лежат асинхронный вызов подпрограммы и принцип неготового значения[
8
].
При асинхронном вызове подпрограммы
![]() из процесса
из процесса
![]() , выполняющего
подпрограмму
, выполняющего
подпрограмму
![]() происходят такие события (рис.
2
) :
происходят такие события (рис.
2
) :
-
порождается параллельный процесс
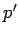 , с подпрограммой
, с подпрограммой
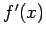
-
выходные переменные
, подпрограммы
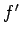 , помещаются в очередь
неготовых значений процесса
, помещаются в очередь
неготовых значений процесса
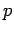 .
.
-
вызвавшая подпрограмму
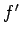 , подпрограмма
, подпрограмма
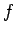 продолжает свою работу
до тех пор, пока ей не понадобятся значения в переменных
, в этом
месте
продолжает свою работу
до тех пор, пока ей не понадобятся значения в переменных
, в этом
месте
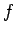 происходит ожидание возврата
происходит ожидание возврата
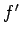 (т. е. синхронизация
процессов
(т. е. синхронизация
процессов
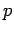 и
и
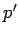 )
)
4.2 Модель последовательной программы
Определим
последовательную многокомпонентную программу
как
упорядоченное множество пар
![]() . Каждая такая пара определяет подпрограмму
в
. Каждая такая пара определяет подпрограмму
в
![]() :
:
где
-
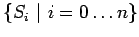 - множество регулярных программ с распределенной памятью
- множество регулярных программ с распределенной памятью
-
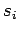 - уникальное имя подпрограммы
- уникальное имя подпрограммы
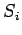 (
(
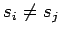 для
для
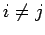 )
)
Введем операторы вызова подпрограммы и возврата из подпрограммы .
-
Оператор
вызова
подпрограммы обозначим
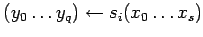
где-
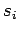 - имя, вызываемой программы
- имя, вызываемой программы
-
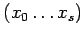 - входные параметры
- входные параметры
-
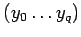 - результаты
- результаты
-
-
Оператор
возврата
из подпрограммы обозначим
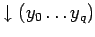 где
где
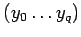 - результаты
- результаты
Процесс выполнения последовательной многокомпонентной программы
![]() описывается дискретной динамической системой
описывается дискретной динамической системой
![]() :
:
Здесь
-
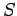 - последовательная многокомпонентная программа (
4
)
- последовательная многокомпонентная программа (
4
)
-
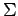 - множество состояний
- множество состояний
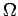
состояние определим так :
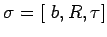
где- - состояние памяти
-
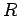 - состояние управления (остаточная программа)
- состояние управления (остаточная программа)
-
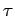 - список вызовов подпрограмм
- список вызовов подпрограмм
- - начальное состояние
-
![$ \Sigma_E=\{\ [\ b,\downarrow(y_0\ldots y_q),\oslash\ ]\ \}$](content/parallel-sequential-program-decomposition.html/img80.gif) - множество заключительных состояний
- множество заключительных состояний
-
Отношение переходов
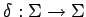 задается следующим образом:
задается следующим образом:
-
выполнение элементарного оператора
:
![$ [\ b,yR,\tau\ ] \Rightarrow [\ y(b),R,\tau\ ]$](content/parallel-sequential-program-decomposition.html/img82.gif)
-
условный переход :
![$ [\ b,(u\rightarrow(R,Q))T,\tau\ ] \Rightarrow
\left\{\begin{aligned}
\lbrack\ ...
... :\ & u(b)=1\\
\lbrack\ b,QT,\tau\ \rbrack\ :\ & u(b)=0
\end{aligned}\right. $](content/parallel-sequential-program-decomposition.html/img83.gif)
-
итерация :
![$ [\ b,u\{R\}Q,\tau\ ]\Rightarrow
\left\{\begin{aligned}
\lbrack\ b,Q,\tau\ \rbr...
...b)=0\\
\lbrack\ b,R\ u\{R\}Q,\tau\ \rbrack\ :\ & u(b)=1
\end{aligned}\right. $](content/parallel-sequential-program-decomposition.html/img84.gif)
-
вызов программы
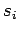 :
:
![$ [\ b_i,f_jR_i,\tau\ ] \Rightarrow
[\ b_j, S_j, [\ b_i ,f_jR_i,\tau\ ] * \tau\ ]$](content/parallel-sequential-program-decomposition.html/img85.gif)
где
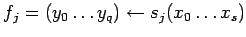 - вызов программы
- вызов программы
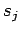
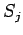 - компонентная программа с именем
- компонентная программа с именем
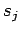
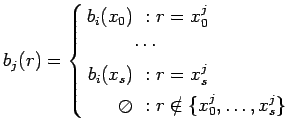
где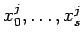 - внутренние переменные
- внутренние переменные
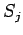 , соответствующие
входам
, соответствующие
входам
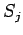
-
возврат из подпрограммы :
![$ [\ b_j,\downarrow(y^j_0\ldots y^j_q),[\ b_i,f_jR_i,\tau\ ]*\tau\ ]
\Rightarrow [\ b_i', R_i, \tau\ ]$](content/parallel-sequential-program-decomposition.html/img91.gif)
где
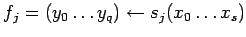 - вызов программы
- вызов программы
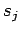
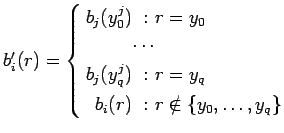
-
выполнение элементарного оператора
:
4.3 Модель параллельной программы
Введем понятие
параллельной программы
и определим его как
упорядоченое множество пар
![]() . Каждая такая пара определяет параллельный
процесс :
. Каждая такая пара определяет параллельный
процесс :
где
-
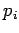 - уникальное имя компоненты
- уникальное имя компоненты
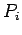 (
(
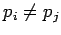 для
для
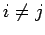 )
)
-
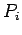 - регулярная программа в алгебре алгоритмов (
3
),
расширенная операторами обмена данными,
- регулярная программа в алгебре алгоритмов (
3
),
расширенная операторами обмена данными,
причем множество является множеством регулярных программ с распределенной памятью
Определим два типа операторов обмена данными между компонентами параллельной программы :
-
синхронные операторы обмена
- обе компоненты
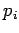 и
и
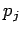 дожидаются завершения транзакции :
дожидаются завершения транзакции :
-
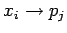 -
синхронная посылка
данных из
внутренней переменной
-
синхронная посылка
данных из
внутренней переменной
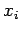 компоненты
компоненты
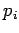 в компоненту
в компоненту
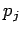
-
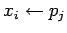 -
синхронный прием
данных из
компоненты
-
синхронный прием
данных из
компоненты
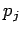 во внутреннюю переменную
во внутреннюю переменную
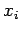 компоненты
компоненты
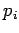
-
-
асинхронные операторы обмена
- после вызова оператора, управление немедленно
возвращается, а данные попадают в очередь на обработку:
-
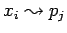 -
асинхронная посылка
данных из
внутренней переменной
-
асинхронная посылка
данных из
внутренней переменной
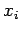 компоненты
компоненты
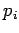 в компоненту
в компоненту
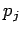
-
Назовем элементарными операторами все операторы, не являющиеся операторами обмена данными между компонентами параллельной программы.
Процесс выполнения последовательной многокомпонентной программы
![]() описывается дискретной динамической системой
описывается дискретной динамической системой
![]() :
:
-
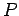 - параллельная программа (
5
)
- параллельная программа (
5
)
-
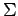 - множество состояний
- множество состояний
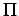
состояние определим так :![$\displaystyle \sigma = [\ (p_0,b_0,R_0),\ldots,(p_n,b_n,R_n),\tau\ ]$](content/parallel-sequential-program-decomposition.html/img104.gif)
где-
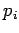 - имя компоненты
- имя компоненты
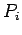 параллельной программы
параллельной программы
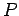
-
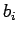 - состояние памяти компоненты
- состояние памяти компоненты
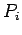
-
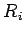 - состояние управления компонентой
- состояние управления компонентой
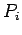
(остаточная программа при выполнении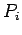 )
)
-
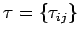 - матрица
- матрица
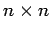 (
(
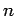 - количество
компонент в
- количество
компонент в
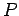 ), где
), где
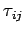 - очередь
значений
переменных
из внутренней памяти
- очередь
значений
переменных
из внутренней памяти
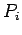 компоненты
компоненты
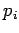 на передачу в компоненту
на передачу в компоненту
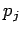 ;
;
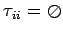
-
-
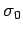 - начальное состояние
- начальное состояние
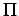 :
:
![$ [\ (p_0, \oslash,P_0),\ldots,(p_n, \oslash,P_n) , \oslash\ ]$](content/parallel-sequential-program-decomposition.html/img113.gif)
-
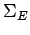 - заключительные состояния
- заключительные состояния
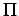 :
:
![$ \{\ [\ (p_0, b_0,\oslash),\ldots,(p_n,b_n,\oslash) , \oslash\ ]\ \}$](content/parallel-sequential-program-decomposition.html/img115.gif)
-
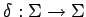 - отношения переходов
- отношения переходов
( фиксируются только используемые части вектора состояния)-
выполнение элементарного оператора
:
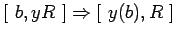
-
условный переход :
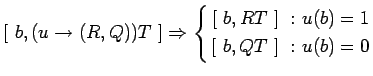
-
итерация :
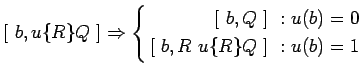
-
синхронный обмен данными
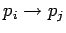 :
:
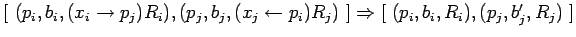
где
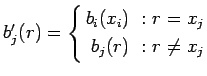
-
асинхронная посылка данных
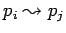 :
:
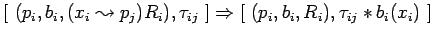
-
доставка данных из очереди
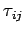 :
:
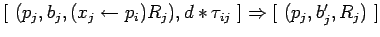
где
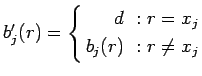
-
выполнение элементарного оператора
:
4.4 Транслятор-распараллеливатель
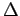
Полуавтоматическая система распараллеливания последовательных программ описывается следующей дискретной динамической системой :
Здесь
-
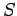 - последовательная многокомпонентная программа (
4
)
- последовательная многокомпонентная программа (
4
)
-
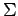 - множество состояний
- множество состояний
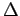
состояние определяется так :![$\displaystyle \sigma=[R,\tau,\mu,\pi,P]$](content/parallel-sequential-program-decomposition.html/img127.gif)
где-
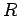 - остаточная программа от
- остаточная программа от
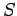
-
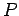 - параллельная программа (
5
)
- параллельная программа (
5
)
-
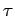 - очередь состояний вызовов последовательной программы
- очередь состояний вызовов последовательной программы
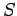 ,
элементами этой очереди есть остаточные программы
,
элементами этой очереди есть остаточные программы
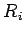
-
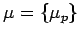 - множество неготовых переменных при выполнении
параллельной программы
- множество неготовых переменных при выполнении
параллельной программы
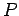 ,
,
где![$ \mu_p=\{\ [(y_0\ldots y_q),p']\ \}$](content/parallel-sequential-program-decomposition.html/img129.gif) - множество неготовых внутренних переменных компоненты
- множество неготовых внутренних переменных компоненты
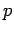 , где
, где
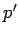 - компонента-поставщик значений для переменных
- компонента-поставщик значений для переменных
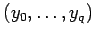
-
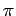 - очередь имён параллельных компонент программы
- очередь имён параллельных компонент программы
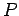
-
-
![$ \sigma_0=[S,\oslash,\oslash,p_0,(p_0,\oslash)]$](content/parallel-sequential-program-decomposition.html/img131.gif) - начальное состояние
- начальное состояние
-
- заключительное состояние
-
Отношения переходов
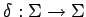 задаются следующим образом:
задаются следующим образом:
введём обозначения :
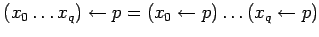
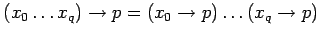
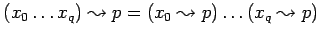
-
трансляция оператора
, не являющийся оператором вызова или возврата :
![$\displaystyle [\ yR,\tau, \mu, (p*\pi), (p,Q)\ ] \Rightarrow
[\ R,\tau, \mu, (p*\pi), (p,Qy)\ ]$](content/parallel-sequential-program-decomposition.html/img136.gif)
-
трансляция оператора вызова программы
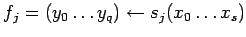 :
:
![$\displaystyle [\ f_jR_i,\tau,\mu_p, (p*\pi), (p,Q)\ ] \Rightarrow
[\ S_j,(R_i*\tau), \mu_p', (p'*p*\pi), P\ ]$](content/parallel-sequential-program-decomposition.html/img137.gif)
где-
- создаём новую параллельную компоненту
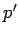 ,
посылаем параметры
,
посылаем параметры
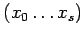 из
из
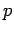 в
в
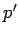 ,
принимаем параметры в
,
принимаем параметры в
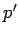 во внутренние переменные
во внутренние переменные
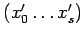
-
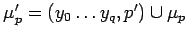 - добавляем в очередь неготовых
переменных
- добавляем в очередь неготовых
переменных
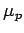 выход
выход
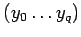 , вызванной программы
, вызванной программы
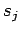
-
- создаём новую параллельную компоненту
-
трансляция оператора возврата из подпрограммы последовательной программы
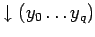 :
:
где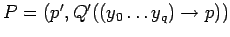
-
обработка неготовой входной переменной :
пусть оператор из компоненты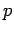 и
и
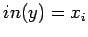
если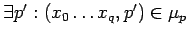 и
и
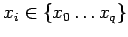 то
то
![$\displaystyle [\ R,\tau,\mu'_p,\pi, (p,QyT)\ ]\Rightarrow
[\ R,\tau,\mu_p,\pi, (p,Q((x_0\ldots x_q)\leftarrow p')yT)\ ]$](content/parallel-sequential-program-decomposition.html/img147.gif)
где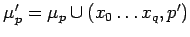
-
трансляция оператора
, не являющийся оператором вызова или возврата :
5 Реализация
Опишем реализацию транслятора-распараллеливателя для языка C.
5.1 Построение кластера
Вычислительные системы сверхвысокой производительности стоят дорого. Цена таких систем недоступна для большинства образовательных и научно-исследовательских организаций, но часто существует приемлемая альтернатива - кластер. При достаточном числе узлов, такие системы способны обеспечить требуемую производительность.
Можно использовать уже существующую сеть рабочих станций (системы такого типа иногда называют COW - Cluster Of Workstations). При этом узлы могут иметь различную архитектуру, производительность, работать под управлением разных OC (MS Windows, Linux, FreeBSD).
Если узлы планируется использовать только в составе кластера, то их можно существенно облегчить (отказаться от жёстких дисков, видеокарт, мониторов и т.п.). В облегчённом варианте узлы будут загружаться и управляться через сеть. Количество узлов и требуемая пропускная способность сети определяется задачами, которые планируется запускать на кластере.
5.2 Стандарт MPI
Message Passing Interface (MPI) - популярный стандарт для построения параллельных программ по модели обмена сообщениями. Этот стандарт обычно используют в параллельных системах с распределённой памятью (кластера и т.п.).
MPI содержит в себе разнообразные функции обмена данными, функции синхронизации параллельных процессов, механизм запуска и завершения параллельной программы. Стандарт MPI-1 описывает статическое распараллеливание, т.е. количество параллельных процессов фиксировано, это ограничение устранено в новом стандарте MPI-2, позволяющем порождать процессы динамически. MPI-2 в настоящее время находится в стадии разработки.
Разными коллективами разработчиков написано несколько программных пакетов, удовлетворяющих спецификации MPI (MPICH, LAM, HPVM etc.). Существуют стандартные ''привязки'' MPI к языкам С, С++, Fortran 77/90, а также реализации почти для всех суперкомпьютерных платформ и сетей рабочих станций.
5.3 Работа с MPI на кластере
В данной работе для прогона контрольных примеров был использован кластер на основе сети персональных компьютеров и библиотека MPICH (http://www-unix.mcs.anl.gov/mpi/mpich), созданная авторами спецификации MPI. Этот пакет можно получить и использовать бесплатно. В состав MPICH входит библиотека программирования, загрузчик приложений, утилиты. Существуют реализации этой коммуникационной библиотеки для многих UNIX-платформ, MS Windows.
Для запуска MPI-программ на гомогенном (состоящего из одинаковых узлов, работающих под одной OS) кластере необходимо выполнить следующие шаги.
-
Инсталлировать MPICH на головной узел (машина, с которой будем запускать MPI-программы) кластера.
Инсталлировать MPICH на
все
узлы кластера обычно
не
требуется
.
-
MPICH использует
rsh
(remote shell) для запуска процессов на
узлах кластера. Поэтому необходимо запустить
на каждом узле
rshd
(remote shell server) и согласовать права доступа.
Для обеспечения более высокого уровня сетевой безопасности можно использовать ssh - OpenSSH remote login client.
-
Компиляция MPI-программы на языке С выполняется
утилитой
mpicc
, представляющей собой надстройку над C-компилятором,
установленным в данной OS.
mpicc myprog.c -o myprog -
Перед запуском ''бинарника''
myprog
необходимо разослать его
на все узлы кластера, причем локальный путь до
myprog
должен быть
одинаковый на всех машинах, например -
/usr/mpibin/myprog
.
Вместо процедуры копирования программы на узлы можно использовать NFS (Network File System) :
- на головной машине запускаем NFS-сервер и открываем каталог с myprog
- на каждом рабочем узле кластера, монтируем NFS головной машины, используя единый для всех узлов локальный путь.
-
Запуск MPI-программы производится командой :
mpirun -machinefile machines -np n myprog- machines - файл, содержащий список узлов кластера
- n - количество параллельных процессов
После команды mpirun , MPICH, используя rsh , запускает n -раз программу myprog на машинах из machines . При запуске каждому процессу присваивается уникальный номер, и далее программа работает исходя из этого номера.
5.4 Реализация системы полуавтоматического распараллеливания
Используя MPI, можно писать эффективные параллельные программы, но
непосредственное программирование в MPI имеет ряд недостатков. MPI можно
назвать ассемблером виртуальной многопроцессорной машины. Написание
MPI-программ требует от программиста специальной подготовки. Кроме того,
MPI-программы, как средство низкого уровня, являются, в значительной
мере, архитектурно зависимыми, что затрудняет их переносимость.
Описанная система полуавтоматического распараллеливания
![]() позволяет решить эти проблемы.
позволяет решить эти проблемы.
Реализация
![]() транслирует программу на расширенном языке
C в параллельную MPI-программу на C.
транслирует программу на расширенном языке
C в параллельную MPI-программу на C.
Для того что бы воспользоваться системой полуавтоматического
распараллеливания
![]() , необходимо выполнить следующие шаги.
, необходимо выполнить следующие шаги.
-
Пользователю необходимо разбить свою последовательную программу
на части, которые могут выполнятся независимо друг от друга. Эти части
записываются в виде пользовательских функций, в заголовки которых
добавляется ключевое слово
asyncron
.
asyncron int my_big_func() { /* just do it :) */ return 0; }Вызов такой функций порождает новый параллельный процесс. Таким образом - количество компонент параллельной программы определяется количеством вызовов асинхронных функций. -
Трансляция выполняется командой
delta
. Кроме текста
MPI - программы, транслятор выдает количество параллельных компонент этой
программы, это число используется утилитой
mpirun
.
$ delta myprog.c > myprog_mpi.c components : 4 $ mpicc myprog_mpi.c -o myprog_mpi $ mpirun -machinefile machines -np 4 myprog_mpi
Важной особенностью данной системы является ''гладкий синтаксис''.
Введение ключевого слова
asyncron
является единственным отличием
языка C
![]() от стандартного C. Программа для распараллеливателя
может, без каких либо изменений, собираться обычным (последовательным)
транслятором языка C, достаточно добавить в заголовок программы
#define asyncron
, в этом случае получается обычная (последовательная) программа.
от стандартного C. Программа для распараллеливателя
может, без каких либо изменений, собираться обычным (последовательным)
транслятором языка C, достаточно добавить в заголовок программы
#define asyncron
, в этом случае получается обычная (последовательная) программа.
Распараллеливатель можно получить [ здесь ]
5.5 Пример
Рассмотрим классический пример параллельного программирования - вычисление
![]() .
Число
.
Число
![]() будем вычислять как определенный интеграл :
будем вычислять как определенный интеграл :
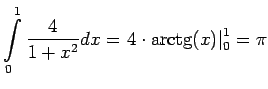
Согласно правилу прямоугольников интеграл можно заменить суммой:
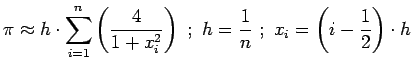
5.5.1 Результаты счета
-
последовательная программа
количество итераций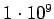
время счета - 108 секунд$ cc pi.c -o pi $ ./pi pi = 3.1415926535899708
-
параллельная программа на двух процессорах
количество итераций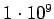
время счета - 57 секунд$ delta pi.c > pi_mpi.c components : 3 $ mpicc pi_mpi.c -o pi_mpi $ mpirun -machinefile machines -np 3 pi_mpi pi = 3.1415926535899708
Программа вычисления
Параллельная MPI-программа вычисления
![]() , результат работы распараллеливателя -- [
pi_mpi.c
]
, результат работы распараллеливателя -- [
pi_mpi.c
]
Литература
-
- 1
-
Задачи для суперкомпьютеров -
http://parallel.ru/research/apps.html
- 2
-
Основные классы современных параллельных компьютеров
-
http://parallel.ru/computers/classes.html
- 3
-
В.В.Воеводин, Вл.В.Воеводин Параллельные вычисления - Санкт-Петербург : БХВ-Петербург, 2002 - 608 стр.
- 4
-
А.Е.Дорошенко Математические модели и методы организации высокопроизводительных параллельных вычислений - Киев : Наукова думка, 2000 - 176 стр.
- 5
-
Коммуникационные библиотеки
-
http://www.parallel.ru/tech/tech_dev/ifaces.html
- 6
-
Средства распознавания параллелизма в алгоритмах
-
http://www.parallel.ru/tech/tech_dev/auto_par.html
- 7
-
Ю.В. Капитонова, А.А. Летичевский Математическая теория проектирования вычислительных систем - Москва : Наука, 1988 - 295 стр.
- 8
- Т-система - http://t-system2.polnet.botik.ru
Evgeny S. Borisov
2004-09-16