
Простая 3D графика.
Е.С.Борисов
1997 г.
Интересующий нас объект может быть представлен в виде связного, регулярного , ациклического графа, т.е. мы как-бы одеваем наш объект в сетку из вершин и дуг графа. При этом, увеличивая число вершин графа можно достичь любой степени достоверности отображения объекта.
Введем две пространственные и одну плоскую систему
координат.
![\includegraphics[width=10cm]{pict/image1.ps}](content/programming-3d-model.html/img1.gif)
- пространственная система OXYZ "вморожена" в объект.
- пространственная система O н X н Y н Z н жестко связана с наблюдателем.
- плоская система O эк X эк Y эк это экран на который мы будем отображать наш объект.
Причем:
- т. O эк лежит между т. O и т. O н
- O эк X эк || O н X н
- O эк Y эк || O н Y н
- O н Y н направлена в т. O
- т. O н в системе OXYZ имеет координаты .
-
заметим что
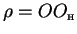 .
.
Рассмотрим произвольную вершину нашего графа М . Пусть в исходной системе OXYZ она имеет координаты M(x,y,z) .
Выполним видовое преобразование. В системе O н X н Y н Z н т. М будет иметь координаты M(x н ,y н ,z н ) .
Матрица перехода V запишется следующим образом :
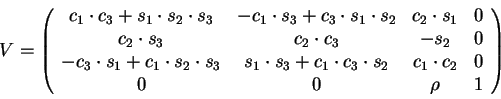
где :
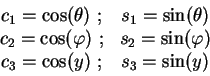
Следующий этап - перспективное преобразование.
![\includegraphics[width=12cm]{pict/image2.ps}](content/programming-3d-model.html/img20.gif)
Для простоты положим
M(x
н
,0,z
н
)
. Из подобия треугольников
следует равенство
или
где d = O н O эк - расстояние от наблюдателя до экрана.
Аналогично :
Таким образом мы получили координаты проекции М на плоскость экрана в системе O эк X эк Y эк .
Обработав все вершины нашего графа ,в результате мы получим вид нашего объекта из нужной нам точки .
Примеры программ:
Литература
-
- 1
- Л.Аммерал ''Принципы программирования в машинной графике.'' Москва, ''Сол Систем'', 1992
Evgeny S. Borisov
2002-11-14
